Números Irracionais – O que são, origem e exemplos

Os números mais simples são os inteiros positivos (1,2,3,4…) usados para contar. Estes são chamados números naturais e são conhecidos há vários milênios. As necessidades básicas do dia-a-dia levaram à introdução de frações como 1/2, 2/3, 5/4, etc. Estes números são chamados racionais. Mas o que são os números irracionais?

O conceito dos números irracionais é totalmente o oposto dos números racionais, em que qualquer número pode ser escrito na forma de fração.

Sendo assim, os números irracionais são aqueles em que os elementos são números decimais, infinitos e não periódicos.

Dessa maneira, eles não podem ser resultado da divisão entre dois números inteiros. Ou seja, não podem ser representados por meio de frações irredutíveis.

Portanto, é fundamental saber que os números irracionais são representados pela letra I (maiúscula).

Origem dos números irracionais

Os números racionais foram criados para fazer a divisão de objetos entre pessoas. Logo depois foi criada a reta numérica, em que cada ponto correspondia a um único número real.

Ao observar bem, os matemáticos notaram que existiam algumas “lacunas” na reta numérica, e que não existiam números racionais que correspondessem com essas lacunas.

Sendo assim, ao longo do tempo, foi descoberto que essas lacunas deveriam ser correspondidas com números decimais infinitos e não periódicos.

Assim também se descobriu, que alguns desses números decimais poderiam ser raízes não exatas.

A descoberta dos números irracionais foi um grande marco nos estudos de geometria. Principalmente quando o assunto é Teorema de Pitágoras, em que a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.

Por exemplo, a medida da diagonal de um quadrado 1×1. Pelo fato da diagonal dividir o quadrado em dois triângulos retângulos, podemos usar o Teorema de Pitágoras para fazer essa conta.

Números Irracionais – O que são, origem e exemplos Conhecimento Científico

Descoberta dos irracionais pelo Teorema de Pitágoras.
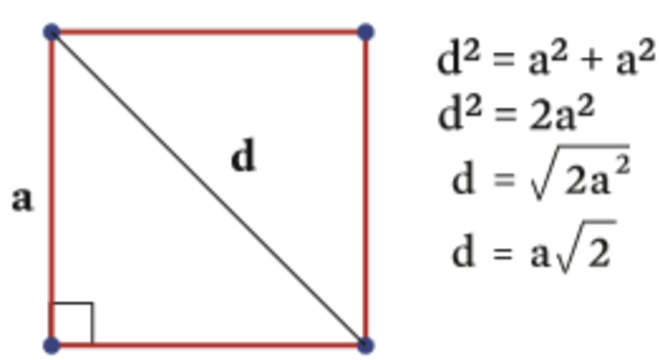
Fonte: Guia do Estudante

Com vimos, a medida da diagonal de um quadrado de lado mediano 1, será  √2. Porém, o resultado dessa raiz é um número decimal infinito e não periódico.

Não conseguimos chegar ao valor da raiz exata, o máximo que conseguimos é um número muito próximo, mas não o valor exato.

Ao extrair sua raiz quadrada, obtemos o seguinte resultado:

√2 = 1,414213562373…. (infinito e não periódico)

Outros exemplos de números irracionais:

√3 = 1,732050807568…. √5 = 2,236067977499… √7 = 2,645751311064…

Teoria dos Conjuntos – Definição, tipos de conjuntos e características

×

Números Irracionais e Dízimas Periódicas

As dízimas periódicas, pelo fato de apresentarem uma representação decimal infinita, elas não podem ser consideradas como números irracionais.

Isso porque, mesmo elas contendo decimais infinitos, elas podem ser representadas por meio de frações. Ou seja, ao contrário do que os números irracionais podem fazer.

Sendo assim, as dízimas periódicas possuem sempre a mesma sequência de repetição.

Um exemplo, o número 0,333… pode ser escrito na forma de fração irredutível, pois:

Conhecimento Científico Conhecimento Científico

Fonte: Toda Matéria

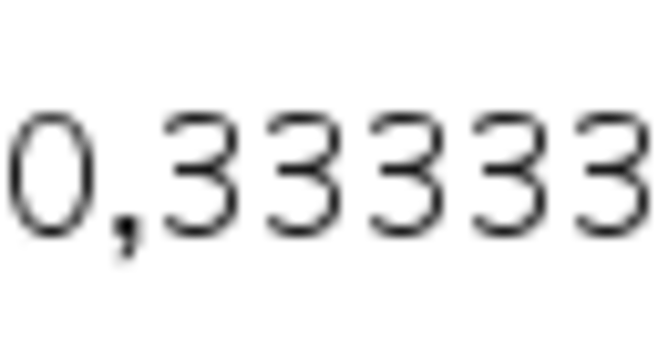
Portanto, as dízimas periódicas são números racionais.

Classificação dos Números Irracionais

Acima de tudo, eles podem ser classificados como algébricos ou transcendentes.

1. Números irracionais algébricos

Será algébrico quando satisfaz uma equação algébrica de coeficientes inteiros, se não for algébrico, então será transcendente.

Como exemplo:

A raiz quadrada de 2 (√2) pode ser escrita como sendo x2 – 2 = 0, então é irracional algébrico.

2. Números irracionais transcendentes

O transcendente é um número real ou complexo que não é raiz de nenhuma equação polinomial a coeficientes inteiros. Um número real ou complexo é assim transcendente somente se ele não for algébrico.

Como exemplo:

O número pi (π), descoberto por meio da divisão do comprimento de uma circunferência pelo diâmetro da mesma. Sendo ele o mais famoso dos números irracionais transcendentes.Π = 3,141592653589793238462… O número de Neper, descoberto por John Napier, representado por e, também é considerado um número irracional transcendente. Sendo aproximadamente igual a 2,718281. O número de ouro (divina proporção), representado por Phi (ϕ). Seu valor é ϕ = 1,618033… E esse número é encontrado através da razão áurea, seguindo a sequencia de Fibonacci.

Conjuntos numéricos

Como visto anteriormente, o conjunto dos números irracionais é representado por I.

O conjunto dos números reais, representado por R, é a união dos números racionais (Q) e números irracionais (I).

Assim, todos os números naturais (N), inteiros (Z), racionais e irracionais são números reais.

Números Irracionais – O que são, origem e exemplos Conhecimento Científico

Gráfico ilustrativo dos conjuntos numéricos.
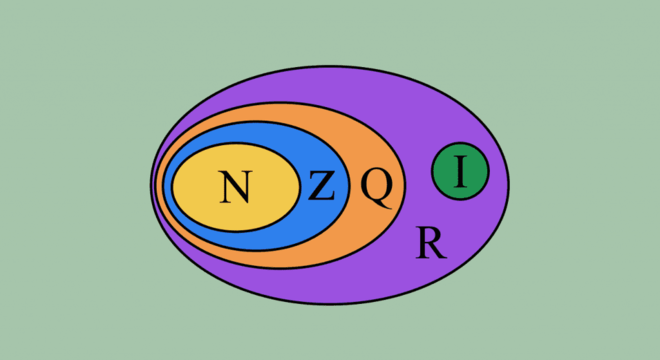
Fonte: Guia do Ensino

Gostou dessa matéria? Agora que tal saber um pouco mais sobre a biografia de Pitágoras.

Fontes: Toda Matéria, Brasil Escola, Mundo Educação 

Fonte Imagem Destacada: Revista Galilleu

Essa matéria Números Irracionais – O que são, origem e exemplos foi criada pelo site Conhecimento Científico.