Quando um número precisa ser multiplicado várias vezes por ele mesmo dá-se o nome de potenciação. Assim, também chamado de exponenciação, a operação visa facilitar a multiplicação de uma série de números iguais.
Dessa forma, ao abreviar uma sequência numérica com fatores iguais, utilizamos a representação an. Nesse sentido, a se refere ao número real. Enquanto isso, n é o número natural. Ou seja, em uma potenciação, existe a base, o expoente e a potência. Assim, quando se tem uma sequência de vários números a potenciação serve para simplificar os cálculos no momento da multiplicação e divisão.
Potenciação e suas propriedades
Em síntese, simplificar as sequências de fatores iguais parece fácil. Porém, a potenciação expressa algumas propriedades que devem ser analisadas. Assim, são pontos importantes para que os erros sejam evitados.
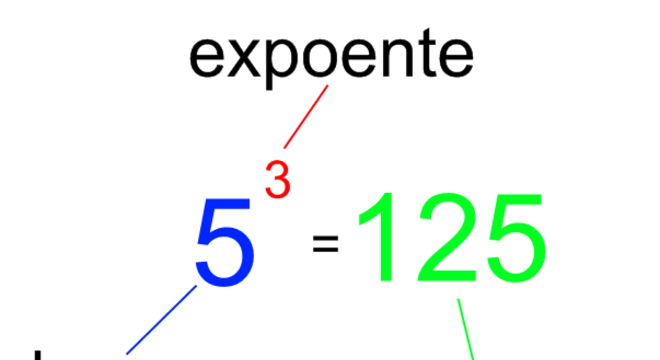
Para se ter uma ideia, a potenciação de uma sequência de fatores iguais é expressa da seguinte forma:
Exemplo:
4³ = 4 x 4 x 4 = 64 5² = 5 x 5 = 25Nesse sentido, em relação a uma potenciação deve-se observar as seguintes características:
Caso a potência possua expoente igual a zero, o resultado será sempre 1. Isso porque, qualquer número elevado à zero é 1; Se a potência possuir expoente no valor de 1, o resultado será o valor da própria base. Isso porque, todo fator elevado a 1 é igual a base; Caso a base da potenciação seja negativa e o expoente um número ímpar, temos um resultado negativo. Ex: (- 3)3 = (- 3) x (- 3) x (- 3) = – 27; Agora, se a base é negativa e o expoente é par o resultado seja positivo. Ex: (- 2)2 = (- 2) x (- 2) = +4; Caso o expoente seja negativo deve-se inverter a base e mudar o sinal do expoente. Ex: (2)– 4 = (1/2)4 = 1/16; Quando a base da potenciação for fração, o numerador e o denominador são elevados ao expoente. Ex: (2/3)3 = (23 / 33) = 8/27Progressões Aritméticas – O que são, fórmulas e maneiras de calcular
×Multiplicação e Divisão de Potências
Em síntese, para operações matemáticas de multiplicação e divisão, a potenciação de fatores segue algumas regras. Dessa forma, para que a multiplicação seja feita é necessário conservar a base das potências quando os números forem iguais. Além disso, soma-se os expoentes. Logo, observe os exemplos: ax . ay = ax+y / 52.53= 52+3= 55
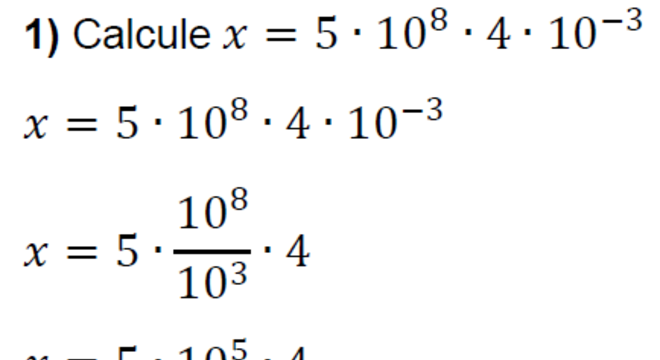
Já em relação à divisão a base também permanece a mesma. Porém, diferente da multiplicação, aqui os expoentes são subtraídos. Dessa forma, observe os exemplos: (ax) / (ay) = ax-y / (53) / (52) = 53-2 = 51
Há ainda o caso da base e o expoente apresentarem mais um expoente fora dos parêntese. Caso isso ocorra, deve-se manter a base e os expoentes são multiplicados. Assim, observe o exemplo: (32)5= 32.5 = 310
O que achou da matéria? Já que está aqui, aproveita pra conferir o que é a Teoria dos Conjuntos e o que são Conjuntos Numéricos.
Fontes: Matemática Básica, Toda Matéria, Só Matemática e Brasil Escola
Fonte imagem destaque: Professor Bruno Fernandes
Essa matéria Potenciação – Definição, propriedades e operações com potências foi criada pelo site Conhecimento Científico.


![Primos fazem SEXO e causa polemica [VÍDEO COMPLETO E SEM TARJAS]](http://3.bp.blogspot.com/-vXjTwuHUrsE/Un_88dXnSrI/AAAAAAAADyM/wxGcIRXYVz4/w72-h72-p-k-no-nu/Sem+t%C3%ADtulo.jpg)



0 Comentários