Seno – Definição, cosseno, tangente, como calcular e características

A trigonometria é responsável por estudar as relações trigonométricas dentro da matemática. Dessa forma, é por meio desse estudo que o triângulo retângulo é analisado e, assim, defini-se o seno, cosseno e a tangente de seus ângulos.

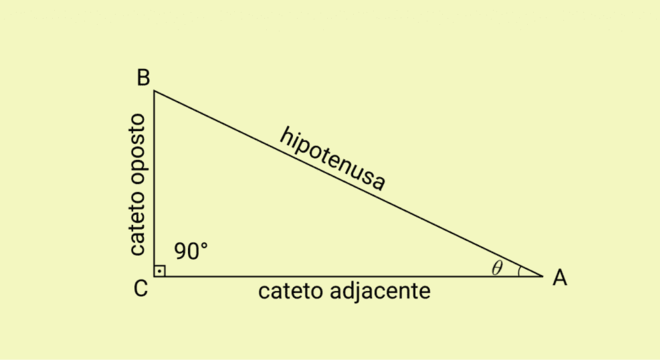
Nesse sentido, um triângulo retângulo é caracterizado por possuir ângulo de 90º. Além disso, os lados que o compõem recebem o nome de cateto e hipotenusa. Visto isso, o seno de um ângulo  é definido calculando a razão existente entre o cateto que está oposto ao ângulo e a hipotenusa.

Além do seno de um triângulo, também é possível calcular o cosseno e a tangente. Juntos, seno, cosseno e tangente, formam a razão trigonométrica de um ângulo. Além disso, os ângulos determinados dentro de triângulo retângulo podem ser opostos ou adjacentes.

Calculando o seno

O seno representa a razão do ângulo entre o cateto oposto à esse ângulo e a hipotenusa. Assim, para que a razão seja encontrada é necessário utilizar a seguinte fórmula que representa o cateto oposto sobre a hipotenusa: sen(α) = cateto oposto a α / hipotenusa

Um ângulo do retângulo triângulo é denominado de agudo. Porém, dentro do triângulo também existem os ângulos notáveis, representados por 30°, 45° e 60°.

Seno - Definição, cosseno, tangente, como calcular e características Conhecimento Científico

O seno é dado pela razão do cateto oposto sobre a hipotenusa. Fonte: Matemática Básica

Visto isso, os ângulos notáveis ficam dispostos no círculo trigonométrico,  onde seno sempre ficará sobre o eixo das ordenadas (y). Dessa forma, contando que o círculo possui 4 quadrantes, o seno será positivo no 1º e 2º e negativo no 3º e 4º quadrantes.

Além disso, em relação aos ângulos notáveis, cada um possui um valor dentro do círculo trigonométrico. Dessa forma, o seno de 30º representa 1/2; 45º equivale a √2/2 e 60º possui valor de √3/2.

Século das luzes – O que foi o iluminismo e sua principal obra

×

Cosseno e Tangente

O cosseno de um triângulo está relacionado a razão do ângulo entre o cateto adjacente e a medida da hipotenusa. Assim como seno, para que a razão seja calculado é necessário utilizar a seguinte fórmula: cos (α) = cateto adjacente / hipotenusa. 

Já em relação à tangente, a razão do ângulo está relacionada à medida do cateto oposto em relação ao cateto adjacente. Logo, para que a razão seja encontrada é necessário utilizar a fórmula: tg (α) = cateto oposto / cateto adjacente. 

Seno - Definição, cosseno, tangente, como calcular e características Conhecimento Científico

Representação do círculo trigonométrico. Fonte: YouTube

Por fim, em relação ao círculo trigonométrico, cosseno e tangente também possuem valores para os ângulos notáveis. Dessa forma, cosseno é representado da seguinte forma: 30º -√3/2; 45º – √2/2; 60º – 1/ 2. Já a tangente recebe os valores de 30º – √3/3; 45° – 1; 60º – √3.

O que achou da matéria? Se gosta de matemática, não deixe de conferir o que são Conjuntos Numéricos e Progressões Geométricas.

Fontes: Toda Matéria, Info Escola e Matemática Básica

Fonte imagem destaque: Estudo Prático

Essa matéria Seno – Definição, cosseno, tangente, como calcular e características foi criada pelo site Conhecimento Científico.