Cubo, o que é? – Composição, diagonais, fórmula da área e volume

A geometria espacial é responsável pelo estudo de diversas formas geométricas. Dentre elas está o cubo, figura geométrica espacial caracterizada como um poliedro regular ou paralelepípedo retângulo. Ou seja, possui as faces e arestas de forma congruente e perpendicular.

Visto isso, o cubo, por ser um poliedro, faz parte do grupo dos Sólidos de Platão. Além do poliedro, também são sólidos as figuras como o tetraedro, o octaedro, o dodecaedro e o icosaedro.

Composição do Cubo

O cubo é uma figura geométrica espacial formado por 12 arestas congruentes – com a mesma medida, 6 faces quadrangulares e 8 vértices. Lembrando que arestas são segmentos de retas, enquanto os vértices estão relacionados aos pontos.

Cubo, o que é? - Composição, diagonais, fórmula da área e volume Conhecimento Científico

Composição do cubo. Fonte: Educa Mais Brasil

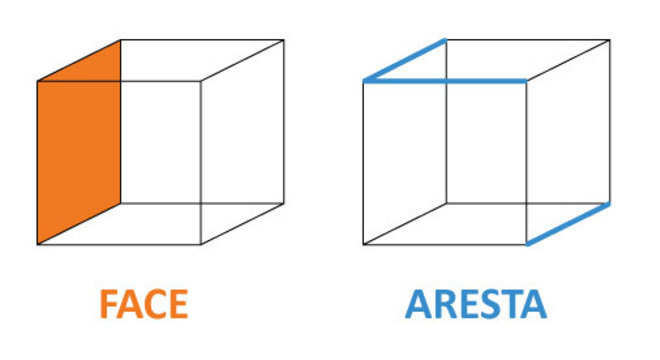
Por ser um poliedro, algumas características são indispensáveis. Isso vale para todos os Sólidos de Platão. Assim, de acordo com estudos de Platão, os poliedros regulares possuem as seguintes características:

Possuem as faces formadas por polígonos regulares e com a mesma medida. No caso do cubo, o quadrado é o polígono regular; Os vértices possuem 3 arestas cada um; Os ângulos possuem a mesma medida, assim, são denominados de congruentes; A fórmula utilizada para calcular a área e o volume levam em consideração a relação de Euler: V – A + F = 2, em que (V) é o número de vértices, (A) é o número de arestas e (F) o número de faces;

Dodecaedro, o que é? Definição, características e significado na geometria

×

Área e volume

Para que a área do cubo seja calculado, devem ser observadas as medidas referentes à área da base, a área lateral e a área total. Nesse sentido, a área da base se refere à medida da área do quadrado.

Ou seja, basta aplicar a fórmula referente à área do quadrado para que a área da base do cubo seja encontrada. Assim, temos: Ab = a². Sendo que, Ab é a área da base e a é a medida da aresta;

Já em relação a área lateral equivale ao cálculo das faces de cima e as de baixo. Para isso, utiliza-se a forma: Al = 4a², em que Al é a área da base e a é a medida da aresta.

Cubo, o que é? - Composição, diagonais, fórmula da área e volume Conhecimento Científico

Exemplo de como se calcula o volume do cubo. Fonte: wikihow

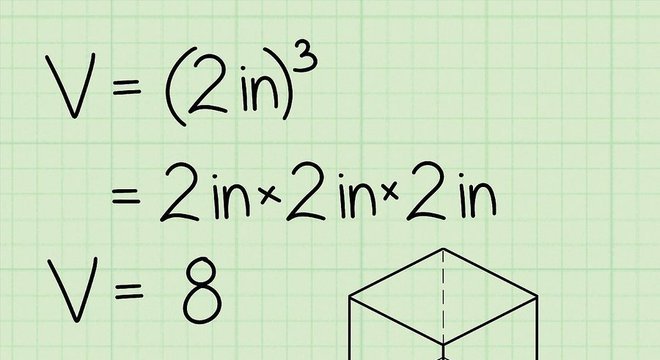
Por outro lado, a área total equivale ao cálculo referente a toda superfície da figura. Assim, calcula-se a área de uma face e multiplica-se esse valor por 6. Assim, temos a seguinte fórmula: At = 6a², em que Até a área da base, enquanto a é a medida da aresta.

Em relação ao volume, o cálculo leva em consideração as medidas do comprimento, largura e altura. Nesse sentido, já que as arestas e faces dos poliedros regulares possuem medidas congruentes, basta pegar um dos valores e elevar à potência 3.

Assim, temos a seguinte fórmula: V = a³, em que V é a medida do volume e a é a medida da aresta. Lembrando que, por ser uma figura tridimensional, a unidade de medida do cubo é o metro cúbico (m³).

Diagonais

Em síntese, o cubo apresenta dois tipos de diagonais. Ou seja, a diagonal da base e a diagonal do cubo.

Nesse sentido, para que a diagonal da base seja calculado, deve-se levar em consideração à medida equivalente a diagonal de um quadrado. Isso porque, a face de um cubo é formada por um quadrado. Dessa forma, utiliza-se o Teorema de Pitágoras para que o cálculo seja feito. Assim, temos: db² = a² + a² ⇒ db² = 2a² ⇒ db = a√2.

Cubo, o que é? - Composição, diagonais, fórmula da área e volume Conhecimento Científico

Diagonal cubo. Fonte: YouTube

Por fim, a diagonal do cubo é calculada levando em consideração o segmento de reta que é traçado de um vértice à outro passando pelo meio da figura. Assim, como na diagonal da base, a diagonal do cubo também pode ser calculada pelo Teorema de Pitágoras. Dessa forma, temos a seguinte fórmula: dc² = a² + d²b ⇒ dc² = a² + 2a² ⇒ dc² = 3a² ⇒ dc = a√3.

Exemplo

Observe o seguinte exemplo:

Um professor de matemática apaixonado por probabilidade resolveu dar de aniversário à sua namorada um pingente em forma de dado folheado a ouro. Sabendo que o valor do ouro é de R$ 0,90 por mm2, que o pingente já vem de fábrica na cor vermelha e que a aresta do cubo do pingente mede 7 mm, responda:

Quanto o professor gastou para deixar duas faces opostas em vermelho, folheando as outras faces?

Visto isso, como resposta, temos:  Duas faces opostas de um cubo são suas bases; as outras são faces laterais. A área lateral de um cubo pode ser obtida pela seguinte fórmula:

Al = 4·l2

Al = 4·72

Al = 4·49

Al = 196 mm2

Desse modo, o professor gastaria 0,9·196 = 176,4 (R$ 176,40) para folhear a área lateral do cubo.

Quanto o professor gastará para folhear o cubo inteiro?

At = 6·l2

At = 6·72

At = 6·49

At = 6·49

At = 294 mm2

O valor gasto será 0,9·294 = 264,6 (R$ 264,60).

O que achou da matéria? Se gostou, confira como calcular a Área do Triângulo e o que é Trigonometria.

Fontes: Toda Matéria, Matemática Básica e Brasil Escola

Fonte imagem destaque: Matemática Básica

Essa matéria Cubo, o que é? – Composição, diagonais, fórmula da área e volume foi criada pelo site Conhecimento Científico.