Operações com frações, é um o conjunto dos números racionais, que fazem parte de um conjunto fechado para as operações de adição, subtração, multiplicação e divisão.
Decerto, na matemática, quando dizemos que um conjunto é fechado para alguma operação, queremos dizer que quando operamos dois elementos desse conjunto o resultado ainda permanece nele. Assim, quando realizamos qualquer operação entre frações, o resultado ainda é uma fração.
Adição de frações
As regras para somar as operações com frações são exatamente as mesmas para subtraí-las. Portanto, quando escrevermos uma regra para adição, ela também será válida para subtração. Decerto, a ideia de adição de frações é idêntica à de adição de números inteiros. A adição de frações são divididas em dois casos. O primeiro envolve apenas frações com denominadores iguais e o segundo envolve frações com denominadores diferentes.
Denominadores iguais
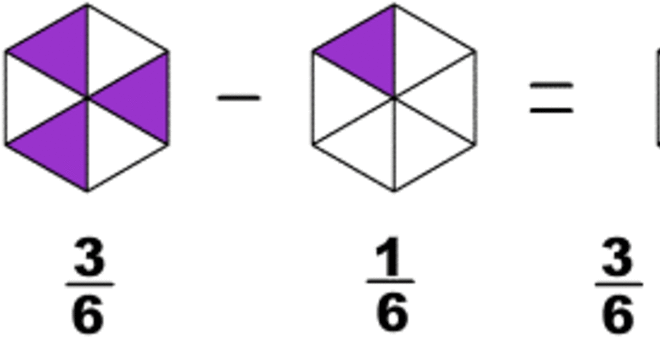
Os cálculos no primeiro caso são fáceis, conserva-se os denominadores e soma-se (ou subtrai-se) apenas o numerador.
Exemplo: 3/7 – 2/7 = 1/7
Denominadores diferentes
Entretanto, o caso em que os denominadores são diferentes é um pouco mais trabalhoso. Na realidade, antes de somar esse tipo de operações com frações, é necessário encontrar frações equivalentes a elas que possuam o mesmo denominador. Assim, para encontrar essas frações equivalentes, existe um método prático no qual o primeiro passo é encontrar o mínimo múltiplo comum entre os denominadores.
Exemplo: 3/4 + 5/9 = 27/36 + 20/36 = 47/36
Observe que 36 é o MMC (mínimo múltiplo comum) de 4 e 9. Após calcularmos o MMC dos denominadores, dividiremos esse número pelos denominadores e depois multiplicaremos o que restou pelos numeradores (aquele macete, divide pelo debaixo e multiplica pelo de cima). Confira:
Exemplo: 7/15 + 3/9
O MMC entre 15 e 9 é 45. Posteriormente, divida 45 por 15 e multiplique o resultado por 7. Assim, isso resultará no numerador da primeira fração equivalente, que será:
7/15 + 3/9 = 21/ 45
Assim, repetindo o procedimento para a segunda fração equivalente, vamos obter:
7/15 + 3/9 = 21/ 45 + 15/45
Para finalizar, basta somar as frações equivalentes com os denominadores iguais:
7/15 + 3/9 = 21/ 45 + 15/45 = 36/45
Projeção ortogonal – O que é, variações e projeções
×Subtração de frações
Decerto, o processo de subtração de frações é praticamente idêntica à da operação de adição. Utilizaremos o mesmo processo algébrico. Entretanto, em vez de somar os denominadores, iremos subtrai-los. Veja:
7/15 – 3/9 = 21/ 45 – 15/45 = 6/45
Multiplicação de operações com frações
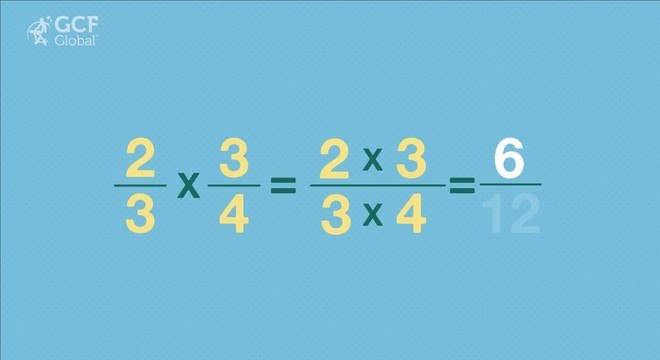
Decerto, a multiplicação entre frações consiste em multiplicar numerador com numerador, em seguida, denominador com denominador delas. Assim, a multiplicação fica da seguinte forma:
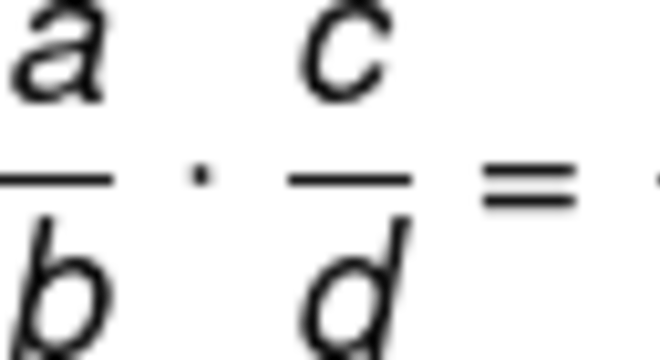
Entretanto, não se esqueça de que, ao final de todas as frações, devemos simplificá-las se possível. Por exemplo:
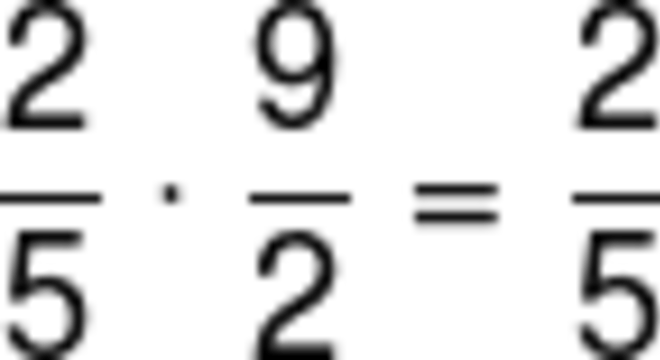
Divisão de frações
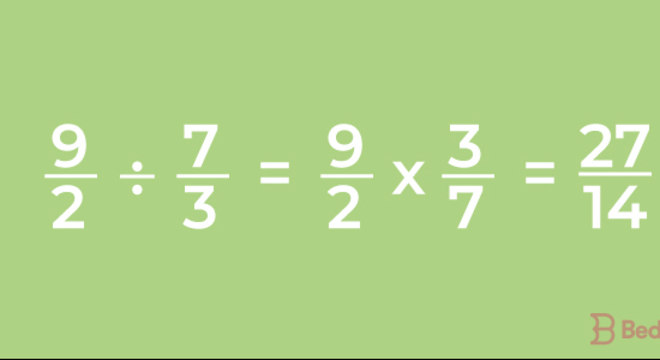
Para dividir duas frações, basta multiplicar a primeira pelo inverso da segunda. Assim, manteremos a primeira equação e iremos inverter a segunda fração. Por exemplo:
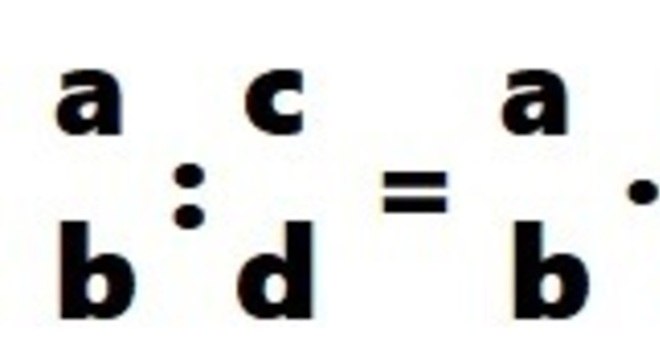
A divisão de frações apresenta duas notações, ou seja, duas maneiras diferentes de representar a mesma ideia, são elas:
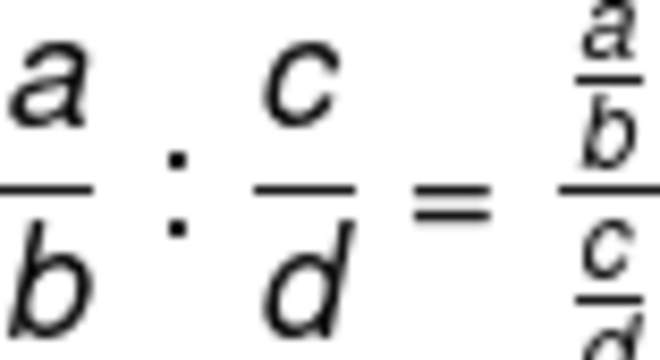
Por exemplo:
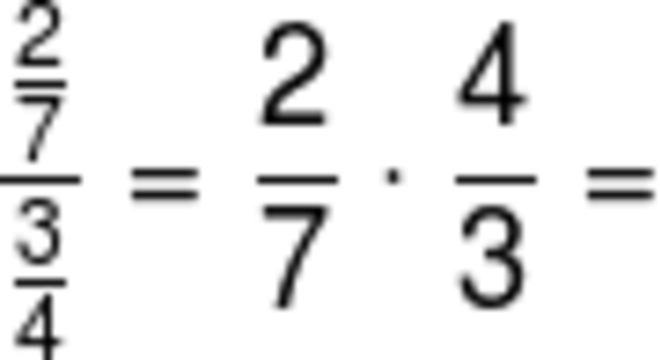
Por fim, leia também sobre Circunferência – O que é, características e geometria analítica
Fonte: Escola kids, Brasil escola, Maxi educa.
Imagem de destaque: Youtube
Essa matéria Operações com frações – Adição, subtração, multiplicação e divisão foi criada pelo site Conhecimento Científico.


![Primos fazem SEXO e causa polemica [VÍDEO COMPLETO E SEM TARJAS]](http://3.bp.blogspot.com/-vXjTwuHUrsE/Un_88dXnSrI/AAAAAAAADyM/wxGcIRXYVz4/w72-h72-p-k-no-nu/Sem+t%C3%ADtulo.jpg)



0 Comentários