Apesar de muitos terem dificuldade e não gostarem dessa ciência, é certo que sem a matemática e suas quatro operações, como a divisão, é impossível realizar atividades corriqueiras do dia a dia.
A divisão, por exemplo, ajuda você a fazer uma compra no supermercado e calcular quanto de troco vai restar, se o seu salário vai ser suficiente para pagar todas as contas do mês e assim por diante.
Porém, o que muitos não sabem, ou não lembram, são as regras que envolvem uma divisão. Para entender como esse processo funciona, é fundamental compreender cada elemento da operação e como chegar em cada um deles.
A divisão e o método da chave
Esse é um dos métodos mais tradicionais e para entende-lo é preciso saber o que é cada elemento do algoritmo.
Digamos que um professor realize uma gincana em uma turma escolar e conte com 38 alunos para serem separados em 4 equipes. Quantos alunos ficarão em cada equipe?
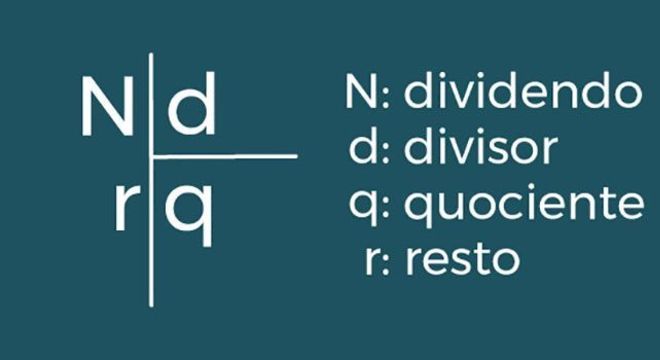
Basta dividir o dividendo 40 (total de alunos) pelo divisor 6 (total de equipes). O resultado dessa conta não é exato, portanto, nem todas as equipes contarão com o mesmo número de participantes.
O resultado, chamado de quociente, será uma média de 6 alunos por equipe, sendo que os outros 4 participantes que sobrarem, ou seja, o resto, deverão ser divididos conforme determinação do professor.
Portanto, em uma divisão nós temos o valor maior (o que irá dividir – dividendo) pelo valor menor (o que será dividido – divisor). O resultado é o quociente e o resto pode ser 0 (quando a divisão for exata) ou maior que 0 (quando há “restos”).
Para aprender como se faz uma divisão, iremos determinar o passo a passo para facilitar o seu processo de aprendizagem.
A divisão com quociente exato
1º) “Arme” a sua conta utilizando o método da chave;
2º) Precisamos descobrir um valor que, multiplicado por 10, resulte em 30 ou chegue o mais próximo possível desse valor. Uma das regras dos critérios de divisibilidade diz que, quando os dois números envolvidos na operação terminam em 0, eles podem ser cortados ao mesmo tempo, sem prejuízo ao resultado.
Portanto, 30 dividido por 10 é o mesmo que 3 dividido por 1. Logo, o nosso quociente é 3 e não há restos. Achou simples? Vamos ao próximo exemplo!
A divisão com quociente decimal
Esse exemplo é um pouco mais complexo, pois não configura uma divisão exata. Nesse caso, o quociente poderia ser exato com um resto ou em forma de número decimal sem resto. Vamos ao passo a passo:
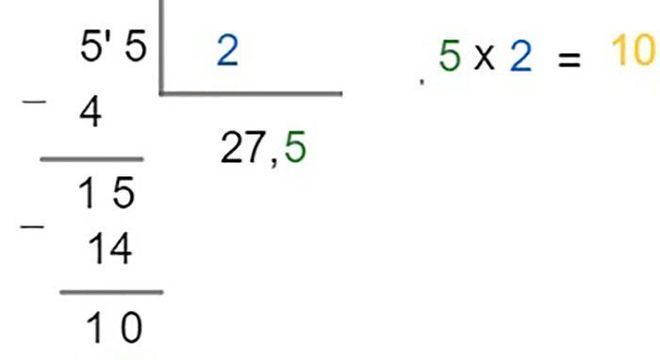
1º) O número 55 é relativamente grande para ser dividido diretamente por 2. Nesse caso, separamos os dois algarismos do dividendo e preferimos dividir primeiro o 5 pelo 2, o que resultou na resposta 2, sobrando o resto 1.
2º) Logo após, puxamos o segundo algarismo 5 para se juntar ao resto 1, já que esse é menor que o dividendo 2. Portanto, formou-se o número 15, que dividido por 2, garantiu um 7 e devolveu 1 de resto (15 -14 = 1)
3º) Como acabaram os algarismos do divisor e ainda sobrou o resto 1, a conta já poderia acabar por aqui, com quociente 27 e resto 1. Porém, a pessoa que respondeu a operação optou por uma quantia mais próxima do resultado final, utilizando a regra de acrescentar o número 0 ao resto 1, uma vez que esse resto é menor que o divisor total.
4º) Divide-se o resto 10 pelo divisor 2, obtendo se o resultado 5 e zerando tudo que sobrou. O resultado final corresponde a 27,5, configurando uma quantia decimal.
Casos em que o dividendo e o divisor não são inteiros
Nesse caso, o ideal é eliminar as vírgulas utilizando a multiplicação por potências de 10, conforme o número de casas.

1º) Multiplica-se ambos (dividendo e divisor) por 100 para que os dois fiquem inteiros. Assim, 1,8 x 100 = 180 e 0,03 x 100 = 3
2º) Divide-se 18 por 3, que tem 6 como resultado. Porém, sobra 0 como resto e, uma vez que não há mais como fazer nenhuma divisão por 3, ele pode ser acrescentado ao consciente.
3º) Portanto, o resultado da conta é 60.
Dicas para aprender a dividir
Dentre as quatro operações, a divisão é a mais trabalhosa. Ela envolve particularidades e regras que precisam ser treinadas e fixadas para que haja a devida aprendizagem. Pensando nisso, trouxemos dicas valiosas para que você aprenda de uma vez por todas a dividir sem medo.
A primeira delas é conhecer bem a tabuada. É fundamental que o aluno tenha domínio da tabuada e das contas de multiplicação para não se atrapalhar ao fazer uma divisão, sobretudo quando a operação envolve números com dois, três ou mais algarismos.
Portanto, estude-a para dominar bem essa ferramenta.
Ademais, uma outra dica importante é conhecer os critérios de divisibilidade. Esses são mecanismos que simplificam a dificuldade em saber se o número 15, por exemplo, é ou não divisível por 5.
A casa do número 5, no critério de divisibilidade, diz que qualquer número terminado em 0 ou 5 é divisível pelo mesmo 5. Isso facilita muito a resolução da conta.
Como dito anteriormente, a próxima dica diz que os números finalizados em zero podem ser “cortados” de cada um dos lados (dividendo e divisor) e em igual quantidade, sem prejuízo ao resultado da conta. Portanto, 1000 dividido por 200 é o mesmo que 10 dividido por 2.
Por último, o uso de frações para simplificar as operações (quando as divisões são grandes) são uma boa opção para facilitar a “quebra de cabeça” no momento do cálculo. Para tanto, deve-se dividir o numerador e denominador da fração pelo mesmo número até que seja possível fazer a divisão.
Se você gostou dessa matéria, confira mais sobre Regra de Sinais entre as quatro operações.
Fontes: Mundo Educação, Brasil Escola, Mundo Educação
Imagens: Freepik, Professor Fagner Sobrinho, Beduka, Escola Kids, Freepik.
Essa matéria Divisão, o que é? Conceito, método da chave e como dividir foi criada pelo site Conhecimento Científico.


![Primos fazem SEXO e causa polemica [VÍDEO COMPLETO E SEM TARJAS]](http://3.bp.blogspot.com/-vXjTwuHUrsE/Un_88dXnSrI/AAAAAAAADyM/wxGcIRXYVz4/w72-h72-p-k-no-nu/Sem+t%C3%ADtulo.jpg)



0 Comentários