O estudo das relações trigonométricas foi fundamental para a disseminação da Matemática. Desse modo, compreende-se que o seno, cosseno e tangente são os nomes dados às razões trigonométricas.
Grande parte dos problemas que envolvem cálculos de distância é resolvida utilizando-se a trigonometria. Portanto, é muito importante compreender seus fundamentos, começando pelo triângulo retângulo.
As razões trigonométricas são também muito importantes, pois elas relacionam as medidas de dois lados do triângulo com um dos ângulos agudos. Sendo assim, associam essa relação com um número real.
Vamos lembrar um pouco do triângulo retângulo antes de começarmos.
O Triangulo Retângulo
O triângulo retângulo é formado por um ângulo de 90° (ângulo reto). Os demais ângulos são menores que 90º, portanto, são agudos.
Além disso, sabemos que os maiores lados estão sempre opostos aos maiores ângulos. Sendo assim, no triângulo retângulo, temos:
Hipotenusa: ela fica oposta ao ângulo reto e é caracterizada por ter o maior lado do triângulo. Catetos: correspondem aos dois outros lados perpendiculares entre si.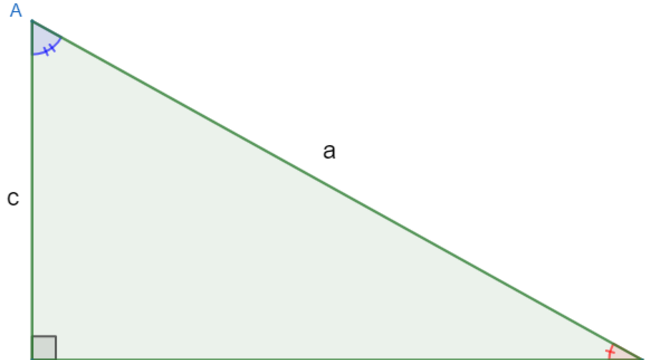
Fonte: Brasil Escola
No triângulo acima, temos que os lados que medem c e b são os catetos, e o lado que mede a é a hipotenusa.
Em todo triângulo retângulo, a relação conhecia como teorema de Pitágoras é válida (a2 = b2 + c2 )
Os catetos, daqui em diante, também receberão nomes especiais. Contudo, as nomenclaturas dos catetos dependerão do ângulo de referência.
Portanto, considerando o ângulo em azul na imagem acima, temos que o cateto que mede b é o cateto oposto, e o cateto que está ao lado do ângulo, ou seja, que mede c é o cateto adjacente.
Números Inteiros – O que são, relação de inclusão e subconjuntos
×A definição de cosseno
O cosseno é uma função trigonométrica periódica limitada obtidas através da razão entre o cateto adjacente e a hipotenusa do triângulo retângulo.
Sendo assim, esta razão entre os lados do triângulo é dado pela fórmula:
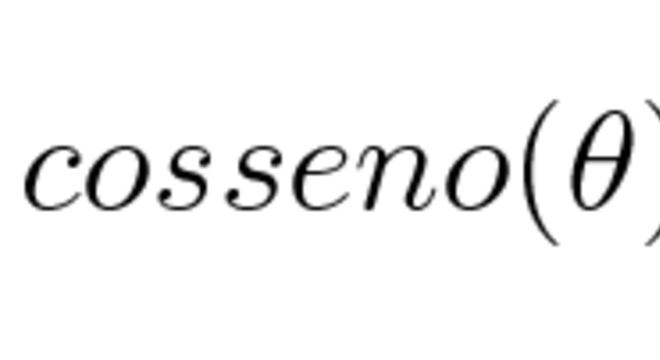
Contudo, a relação cosseno depende do ângulo considerado, veja:
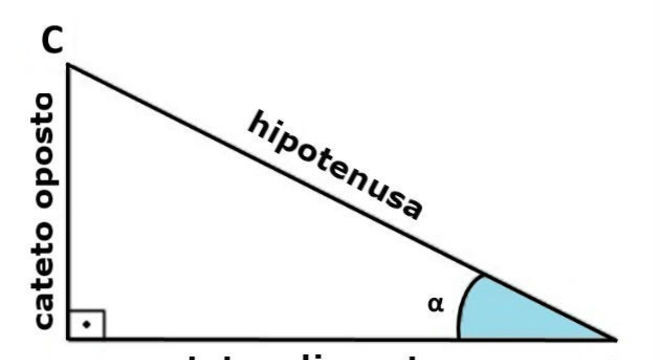
Assim sendo, em relação ao ângulo α, temos:
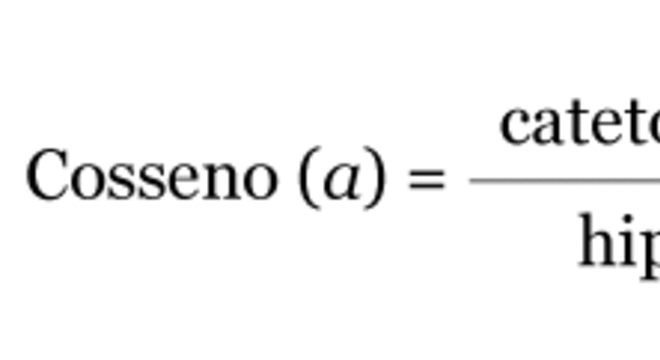
Cosseno dos ângulos notáveis
Existem alguns ângulos que chamamos de notáveis, pois o valor do ângulo é facilmente calculável.
Sendo assim, vamos conhecer os ângulos notáveis do cosseno:
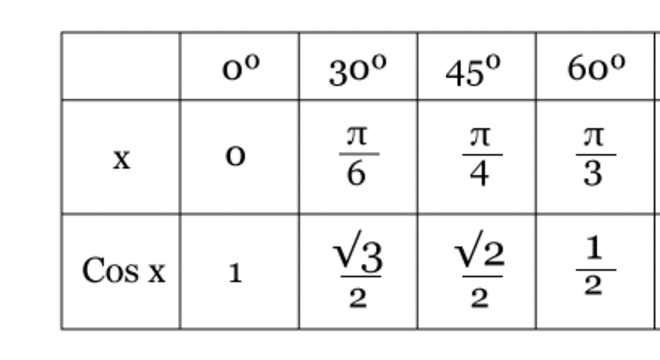
Fonte: Guia Estudo
Função cosseno
Definimos a função cosseno como f(x)=cos(x).
Sendo assim, observe a baixo:
Obs.: Vale lembrar que no primeiro e segundo quadrante a função f é decrescente, ao passo que, no terceiro e quarto quadrantes, a função f é crescente.
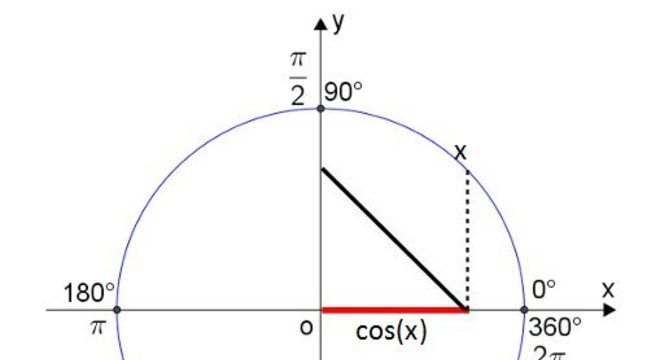
Na função temos que:
O cosseno de um ângulo sempre estará sob o eixo das abscissas (x). Ele é positivo no 1º e 4º quadrantes; Portanto, no 2º e 3º quadrantes os valores são negativos; Domínio da função cosseno diz respeito ao conjunto dos números reais; A imagem corresponde ao intervalo real [-1,1] ou -1 = cos x = 1; O período é o mesmo que a função do seno, sendo assim, é: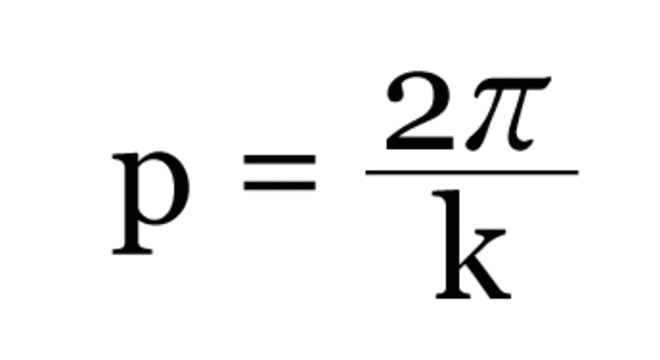
Gráfico da função cosseno
A cossenoide é o nome dado para o gráfico da função cosseno. Sendo assim, veja a seguir sua representação:
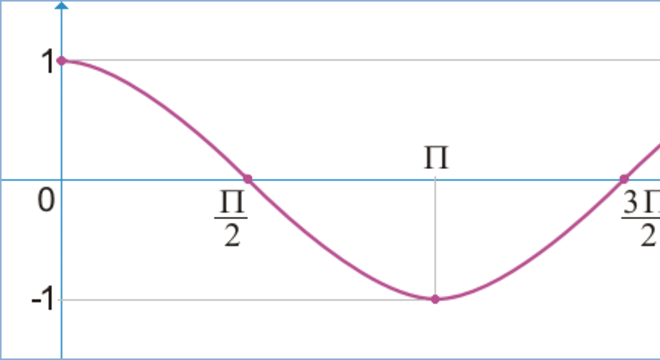
Fonte: Glouny
A lei dos cossenos
A lei dos cossenos é colocada em prática com o intuito de resolver questões trigonométricas quando não trata-se de um triângulo retângulo (que possui ângulo de 90°).
Portanto, usa-se essa lei para resolver cálculos de um triângulo qualquer. Confira abaixo a expressão matemática da lei:
a² = b² + c² – 2ab . CoA
b² = a + c² – 2ac . CosB
c² = a + b² – 2ac . CosC
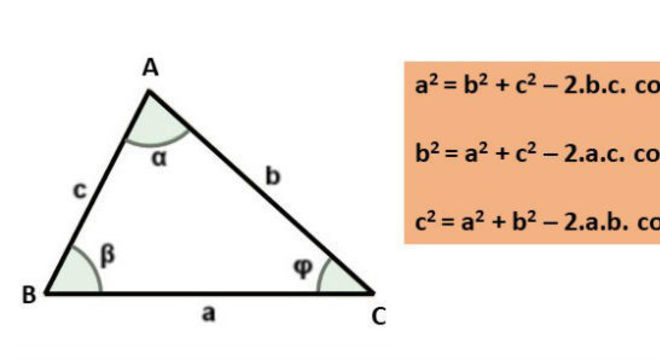
Fonte: Toda Matéria
Exercício
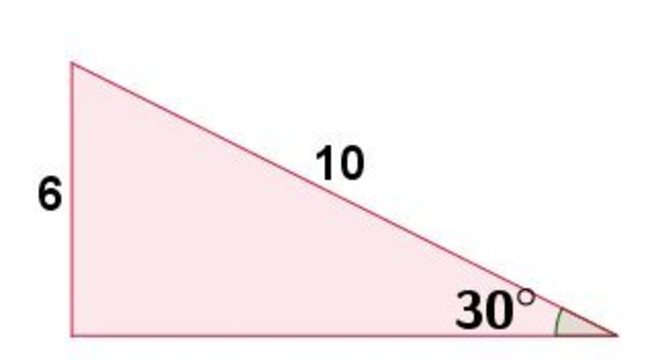
Calcule a medida de x no seguinte triângulo, sabendo que
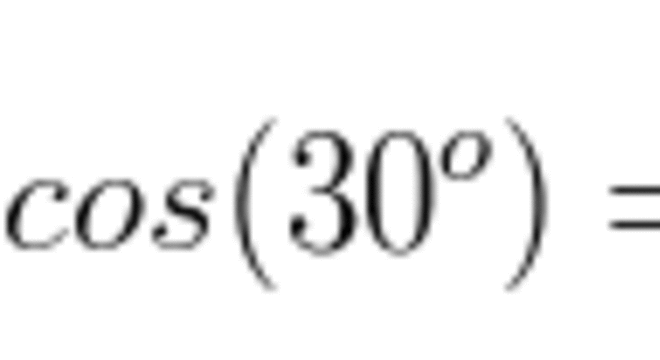
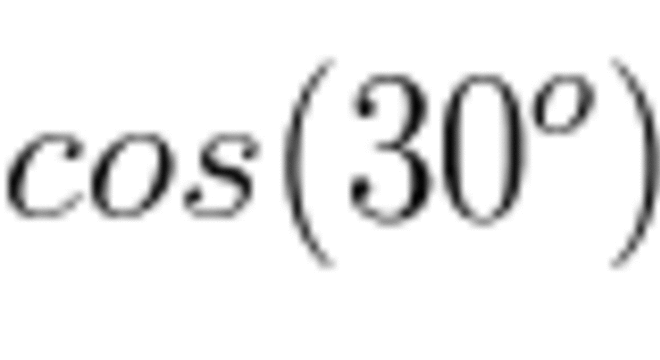
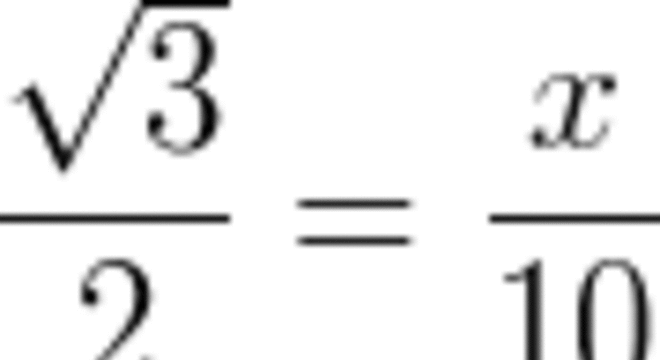
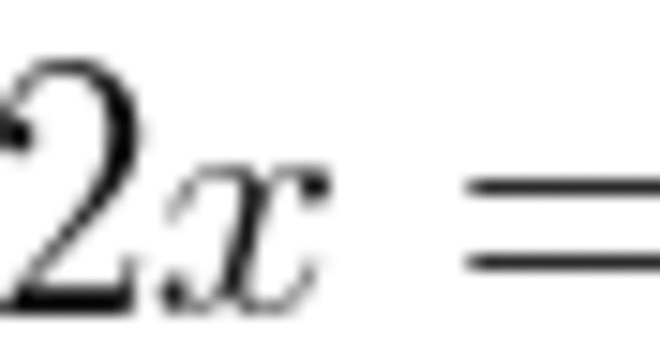
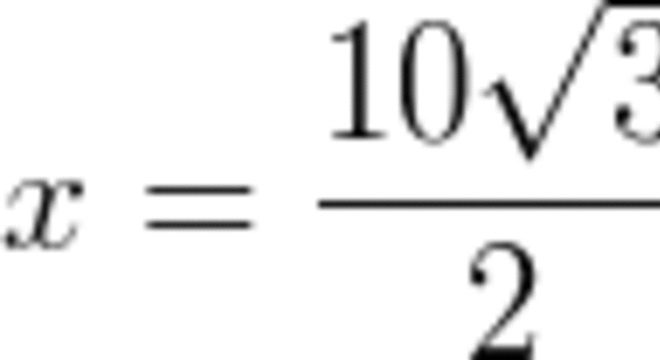
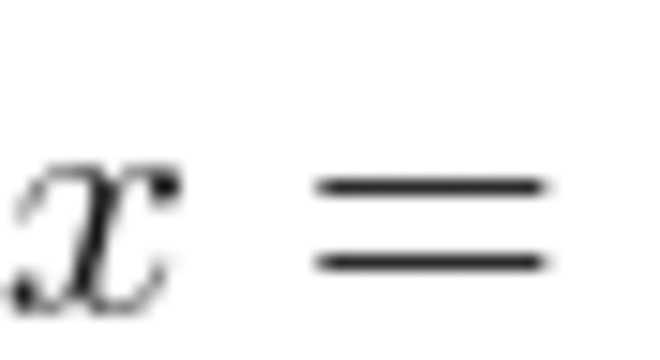
Gostou de entender tudo sobre os cossenos? Em seguida, fique por dentro das Expressões Numéricas.
Fontes: InfoEscola, Educa Mais Brasil, SBM
Fonte Imagem Destaque: Valente Sho
Essa matéria Cosseno – Definição, gráfico da função, tabela e Lei dos Cossenos foi criada pelo site Conhecimento Científico.


![Primos fazem SEXO e causa polemica [VÍDEO COMPLETO E SEM TARJAS]](http://3.bp.blogspot.com/-vXjTwuHUrsE/Un_88dXnSrI/AAAAAAAADyM/wxGcIRXYVz4/w72-h72-p-k-no-nu/Sem+t%C3%ADtulo.jpg)



0 Comentários