Diagonal do quadrado – Definição, Teorema de Pitágoras e exemplos

Quadrado é um polígono que possui os lados iguais e ângulos na mesma medida. Ou seja, é um quadrilátero. Assim, a diagonal do quadrado corresponde aos segmentos de reta responsáveis por ligar dois vértices. Entretanto, os vértices não fazem relação com os lados do quadrado.

Nesse sentido, observando a estrutura desse polígono é possível perceber que só existem duas diagonais. Isso porque, o quadrado é formado por quatro lados congruentes e perpendiculares. Dessa forma, para que o cálculo da diagonal seja feito é possível utilizar duas fórmulas, o Teorema de Pitágoras ou pelo processo de racionalização.

Assim, ao aplicar o Teorema de Pitágoras é possível notar que o quadrado se divide em dois triângulos retângulos. Isso porque, Pitágoras desenvolveu o teorema aplicando os cálculos em um triângulo retângulo. Assim, o triângulo possui dois catetos e uma hipotenusa. Por outro lado, um quadrado possui dois seguimentos de reta que juntam os vértices da figura.

Diagonal do Quadrado

Como já vimos, existem duas maneiras para se calcular a diagonal do quadrado. Uma delas se dá pelo Teorema de Pitágoras, responsável por definir as medidas do comprimento dos lados de um triângulo retângulo. Porém, a mesma regra pode ser aplicada ao quadrado.

Teorema de Pitágoras

Para que o cálculo da diagonal do quadrado seja feita utilizando o Teorema de Pitágoras, basta traçar uma reta que ligue os vértices do polígono. Ou seja, o quadrado será dividido em dois triângulos retângulos. Dessa forma, basta calcular a hipotenusa referente ao triângulo isósceles retângulo.

Diagonal do quadrado - Definição, Teorema de Pitágoras e exemplos Conhecimento Científico

Teorema de Pitágoras. Fonte: Escola Educação

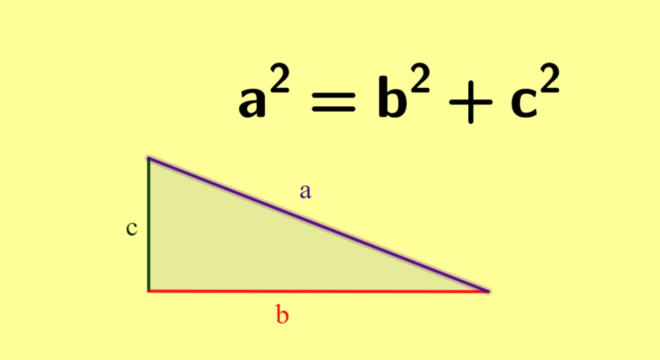
Assim, para que o cálculo seja feito é necessário utilizar a seguinte fórmula: d2 = l2 + l2, aplicando quando o quadrado for divido em triângulo retângulo.

A outra forma de calcular a diagonal do quadrado é pelo processo de racionalização, ou seja, a fórmula transforma o o denominador irracional em um número racional. Nesse sentido, temos: d = l√2.

Racionalização de denominadores – O que é e possíveis racionalizações

×

Exemplos

Para que a explicação seja simplificada, observe os exemplos:

Em um quadrado, traça-se um reta ligando os vértices do polígono. Assim, forma-se um triângulo, que chamaremos de triângulo ABC. Dessa forma, os lados do quadrado se transformam em catetos (os dois lados do triângulo) e uma hipotenusa, a diagonal do quadrado. Assim, temos:

d2 = a2 + a2

d2 = 2a2

d = √2a2

d = a√2

Diagonal do quadrado - Definição, Teorema de Pitágoras e exemplos Conhecimento Científico

Diagonal que liga dois vértices do quadrado. Fonte: Exercícios e soluções

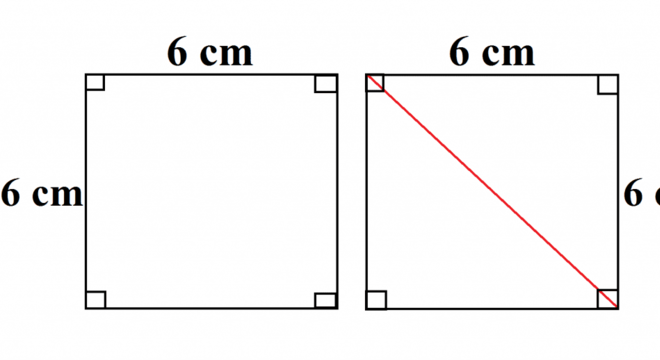
Agora, suponhamos que o lado do quadrado possui lado com medida de 6cm. Utilizando a fórmula do Teorema de Pitágoras, podemos concluir que:

d² = a² + a² d² = 6² + 6² d = 6√2 d = 8,46 cm Definições do Teorema de Pitágoras

O Teorema de Pitágoras foi desenvolvido por Pitágoras, no século VI a.C. A partir dos estudos desenvolvidos pelo filósofo e matemático, definiu-se conceitos como triângulo retângulo, cateto e hipotenusa. Assim, os cálculos da diagonal do quadrado dependem do entendimento desses conceitos.

Triângulo retângulo: corresponde ao triângulo que possui dois ângulos retos, ou seja, de 90º Cateto: menores lados de um triângulo. Além disso, formam o ângulo de 90º. Hipotenusa: maior lado de um triângulo.

O que achou da matéria? Se gosta de matemática, então você não pode deixar de conferir o que é Raiz Quadrada e como as Expressões Numéricas são classificadas.

Fontes: Mundo Educação, Alunos Online e UmComo

Fonte imagem destaque: Matemática Básica

Essa matéria Diagonal do quadrado – Definição, Teorema de Pitágoras e exemplos foi criada pelo site Conhecimento Científico.