Números Inteiros – O que são, relação de inclusão e subconjuntos

Primeiramente, o conjunto dos números inteiros é formado por todos os números que não são decimais. Ou seja, é formado pelos números naturais e os opostos aditivos. Resumindo, é composto por números inteiros positivos e negativos.

Além disso, estes números formam o conjunto dos números inteiros, indicado por ℤ.

O conjunto destes números é infinito dos dois lados, tanto para negativos quanto para positivos; são representados assim:

ℤ = {…,- 3, – 2, – 1, 0, 1, 2, 3,…}

Como podemos observar acima, os inteiros negativos sempre são acompanhados pelo sinal de menos (-), enquanto os inteiros positivos podem ter o sinal de mais (+), porém são emitidos sem prejudicar a compreensão.

O zero é um número neutro, ou seja, não é um número nem positivo e nem negativo.

Outro ponto importante é que os números inteiros possuem um antecessor e sucessor. O sucessor é sempre aquele número que vem depois dele.

Por exemplo: o sucessor do número positivo 2, é o 3. Porém, o sucessor do número -2 é o -2, pois -1 vem depois de -2.

Outro exemplo: o antecessor de -3 é -4, e já o seu sucessor é o -2

Relação de Inclusão

Os conjuntos numéricos podem ser representados pelo diagrama de Venn. Na representação a baixo, conclui-se que a relação de inclusão no conjunto dos inteiros envolve o conjunto dos números naturais (ℕ) junto com os números negativos.

Conhecimento Científico Conhecimento Científico

A relação de inclusão no conjunto dos inteiros envolve o conjunto dos números naturais (N).
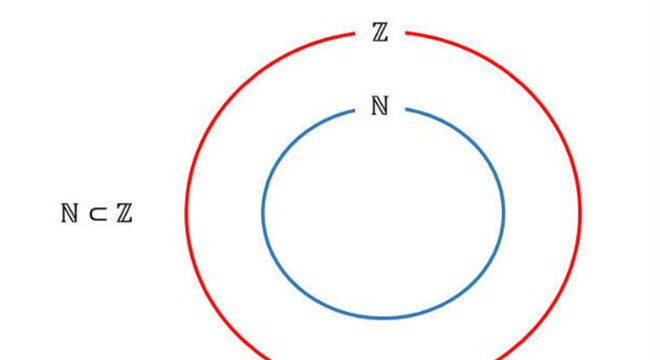
Fonte: Toda Matéria

Sendo assim, se um número é natural, então, ele também é inteiro.

Racionalização de denominadores – O que é e possíveis racionalizações

×

Representação na reta numérica

Os números inteiros podem ser colocados sobre uma reta numérica.

Sendo assim, basta identificar o número zero, chamado de origem, e escolher uma unidade de medida marcando os números inteiros sobre a reta.

A única regra para a construção dessa reta é que os números sejam colocados em sequência crescente, da direita para a esquerda, assim como na reta abaixo:

Conhecimento Científico Conhecimento Científico

Números inteiros na reta numérica.
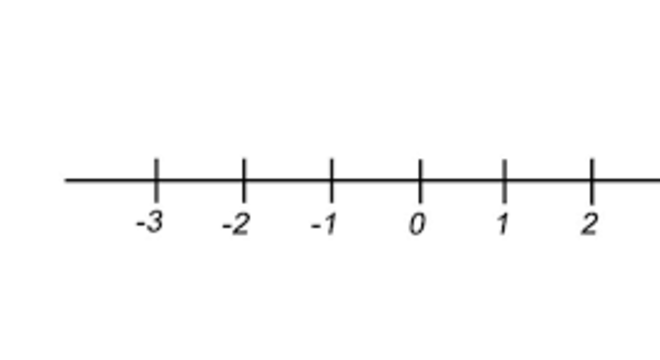
Fonte: Escola Educação

Para exemplificar como os inteiros negativos são opostos aos inteiros positivos, podemos representá-los em uma reta numérica, nesta reta, os números negativos ficam antes do zero e os positivos depois do zero.

Existe também uma simetria entre os números, por exemplo, o número -3 tem a mesma distancia para o zero que o número 3.

Ou seja, os números que estão a uma mesma distância do zero, são chamados de opostos ou simétricos.

Subconjuntos dos números inteiros

É possível encontrar, dentro do conjunto dos números inteiros, outros subconjuntos que são interessantes, como:

ℤ* : é o subconjunto dos números inteiros, com exceção do zero, ou seja, ℤ* = {…, -3,-2,-1, 1, 2, 3, 4, …} ℤ+ : Conjunto dos inteiros não negativos, ou seja, ℤ+ = {0, 1, 2, 3, 4, …} ℤ*+ : é o subconjunto dos inteiros, com exceção dos negativos e do zero. ℤ*+ = {1,2,3,4, 5…} ℤ _ : é o subconjunto dos inteiros não-positivos, ou seja, ℤ_= {…, -4,-3,-2,-1, 0} ℤ*_ : são os números inteiros, com exceção dos positivos e do zero, ou seja ℤ*_= {…, -4,-3,-2,-1}.

Utilizar o (*) significa que o número zero não pertence ao conjunto.

Conhecimento Científico Conhecimento Científico

Subconjunto de N contido em Z nos números inteiros.
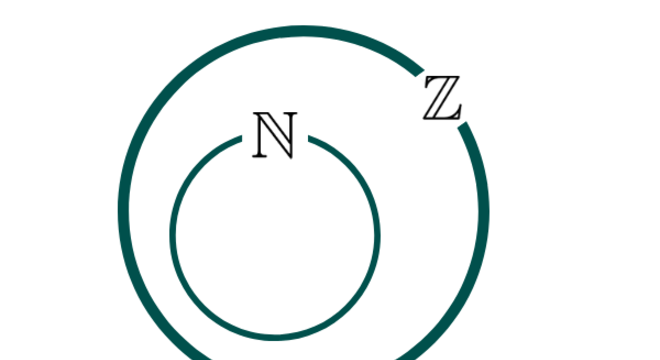
Fonte: Portal Exatas

Divisibilidade

Um número inteiro x, com x ≠ 0, é divisível por outro número y, se a divisão destes números for exata, isto é, possuir resto zero.

Exemplos:

12 é divisor de 4, pois 12 ÷ 4 = 3. 8 é divisor de 2, pois 8 ÷ 2 = 4.

Quando isto ocorre, dizemos que y é divisível por x ou que y é múltiplo de x.

 

 

Conhecimento Científico Conhecimento Científico

Fonte: 2 em 1 Comunicação e Educação

Exercícios de números inteiros

Exercício 1

Considere o conjunto A = {-8, -2, 0, 1/2, 5, 9}, indique neste conjunto quais números pertencem ao conjunto dos inteiros.

Resposta: O conjunto dos inteiros são representados por  Z = {…, -2, -1, 0, 1, 2, …}.  As reticências indicam que o conjunto é infinito para os dois lados. Então, temos que os inteiros são os números negativos e positivos, mais o zero. Portanto, no conjunto A acima, temos que -8, -2, 0, 5 e 9 são números inteiros.

Exercício 2

Calcule a diferença entre os inteiros positivos com o conjunto dos números inteiros.

Resposta: Os inteiros positivos é representado por Z+ = {0, 1, 2, 3, 4, 5, 6, …}.

Portanto, Z – Z+ = {x ∈ Z | X ≤ 0} ou Z = {…, -6, -5, -4, -3, -2, -1}

Exercício 3

Encontre o sucessor e o antecessor dos números inteiros a seguir:

a) 26 = antecessor: x – 1 = 26 – 1 = 25

sucessor: x + 1 = 26 + 1 = 27

b) -84 = antecessor: x – 1 = -84 – 1 = -85

sucessor: x + 1 = -84 + 1 = -83

c) 203 = antecessor: x – 1 = 203 – 1 = 202

sucessor: x + 1 = 203 + 1 = 204

d) -3 = antecessor: x – 1 = -3 – 1 = -4

sucessor: x + 1 = -3 + 1 = -2

e) 0 = antecessor: x – 1 = 0 – 1 = -1

sucessor: x + 1 = 0 + 1 = 1

Com esses exercícios podemos entender um pouco mais sobre a matéria. Bons estudos!

Assim como é importante saber sobre os números inteiros, os números primos também merecem devida importância! Fique ligado.

Fontes: Toda Matéria, Brasil Escola, InfoEscola, Matemática Básica

Fonte Imagem Destacada: CPB Educacional

 

Essa matéria Números Inteiros – O que são, relação de inclusão e subconjuntos foi criada pelo site Conhecimento Científico.