A racionalização de denominadores é um procedimento cujo objetivo é transformar uma fração com denominador irracional em uma fração equivalente com denominador racional.
De maneira mais simples, consiste em transformar um denominador irracional em um número racional, mas sem alterar o valor numérico de uma fração.
Além disso, a racionalização de denominadores simplifica a execução dos cálculos, tornando-os mais rápidos de efetuar.
Como é feita a racionalização de denominadores?
Considere a fração

Vamos agora multiplicar o numerador e o denominador desta fração por

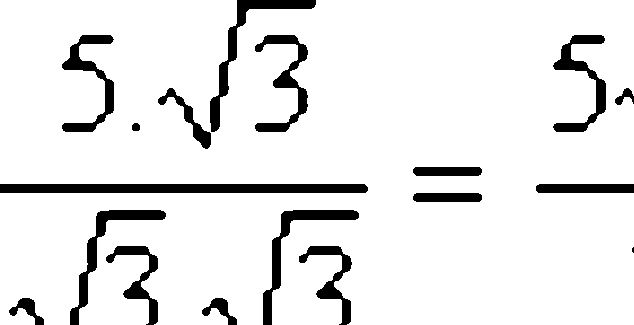
Sendo assim, repare que a fração equivalente

E assim é feita a famosa racionalização de denominadores, que consiste na obtenção de uma fração com denominador racional, equivalente a uma anterior.
Portanto, como observado, racionalizar consiste em multiplicar o denominador e o numerador por um mesmo número. O número escolhido para isso é chamado de conjugado.
Tangente – Definição, gráfico da função, tabela e Lei das tangentes
×Conjugado de um número
O conjugado do número irracional é aquele que ao ser multiplicado pelo irracional dará como resultado um número sem raiz, ou seja, um número racional.
É importante saber, que quando o número for raiz quadrada, o conjugado será igual a própria raiz. Isso porque a multiplicação do número por ele mesmo é igual ao número elevado ao quadrado. Desta forma, é possível eliminar a raiz, tornando assim um número racional.
Exemplo: Encontre o conjugado da raiz quadrada de 2.
Como visto anteriormente, o conjugado da raiz de dois é a própria raiz de dois. Sendo assim:
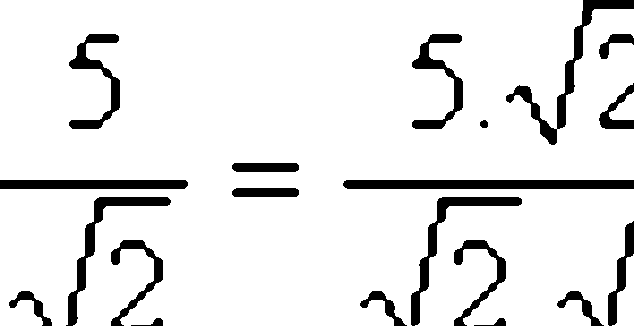
Obs.: Quando a raiz apresentar índice diferente de 2, o conjugado terá o mesmo índice da raiz. Porém, será necessário encontrar o expoente que, somado ao expoente do número inicial, dê como resultado um valor igual ao índice da raiz.
Racionalizando uma fração
Para racionalizar uma fração, devemos seguir os seguintes passos:
Encontrar o conjugado do denominador. Como vimos, o conjugado deve ser tal que elimine a raiz do denominador; Multiplicar o conjugado em cima e embaixo da fração; Simplificar a fração equivalente encontrada.Vamos aos exemplos para melhor entendimento:
Exemplo 1: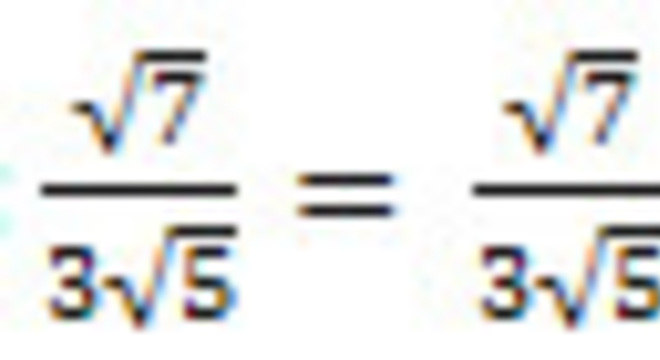
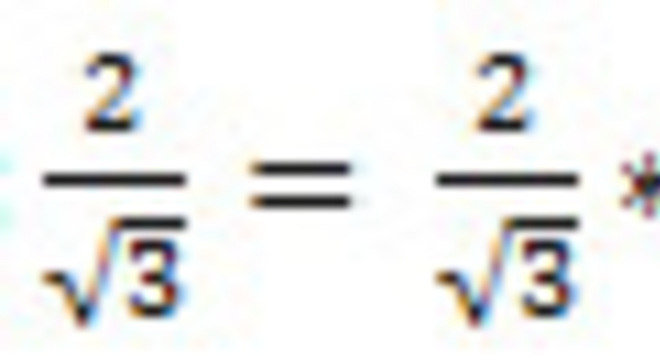
Já quando o denominador é um radical de índice diferente de 2, ou a soma (ou diferença) de dois termos, é necessário multiplicar o numerador e o denominador da fração por um termo conveniente. Só assim para desaparecer o radical que se encontra no dominador.
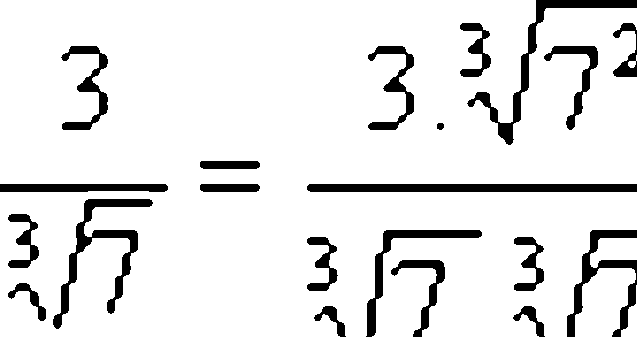
Agora, quando o denominador é composto por uma adição ou uma subtração envolvendo alguma raiz quadrada, o processo é um pouco diferente. Nesses casos é mais prático utilizar as propriedades do produto da soma pela diferença dos mesmos termos.
Assim, se o denominador envolve uma adição, multiplicaremos a fração pela diferença dos termos no denominador e vice-versa.
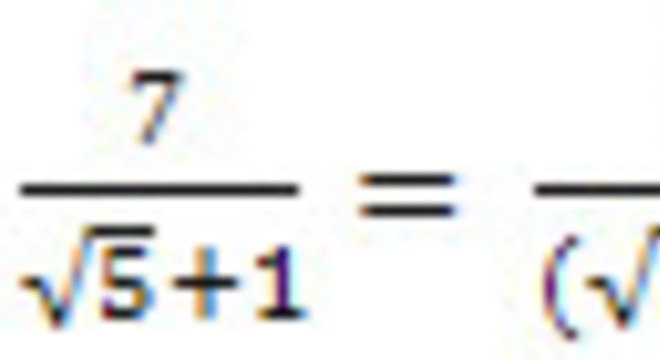
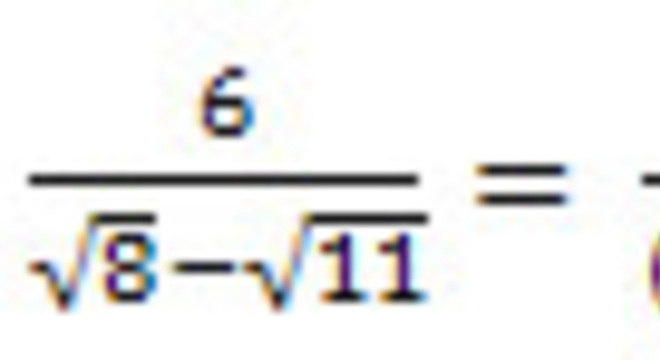
Agora não existe mais dúvidas sobre como usar a racionalização de de dominantes né? Que tal aprender agora sobre os números racionais.
Fontes: Toda Matéria, Brasil Escola, Só Matemática
Fonte Imagem Destaque: Wiki How
Essa matéria Racionalização de denominadores – O que é e possíveis racionalizações foi criada pelo site Conhecimento Científico.


![Primos fazem SEXO e causa polemica [VÍDEO COMPLETO E SEM TARJAS]](http://3.bp.blogspot.com/-vXjTwuHUrsE/Un_88dXnSrI/AAAAAAAADyM/wxGcIRXYVz4/w72-h72-p-k-no-nu/Sem+t%C3%ADtulo.jpg)



0 Comentários