Primeiramente, a trigonometria estuda as relações entre os lados e os ângulos de um triângulo. Em contraste, as funções trigonométricas referem-se aos ângulos retângulos. Desse modo, são elas: seno, cosseno e tangente.
Cosseno é a divisão entre cateto adjacente e hipotenusa e seno é a razão entre cateto oposto e hipotenusa. Já a tangente, diz respeito apenas à divisão entre os catetos.
Sendo assim, ela é uma função trigonométrica calculada a partir da divisão entre os catetos oposto e adjacente de um triângulo retângulo.
Em seguida você vai entender melhor.
Tangente de um ângulo
A tangente de um ângulo é uma função trigonométrica periódica limitada obtidas através da razão entre o Cateto Oposto e o Cateto adjacente do triangulo retângulo.
Contudo, a relação depende do ângulo considerado, veja:
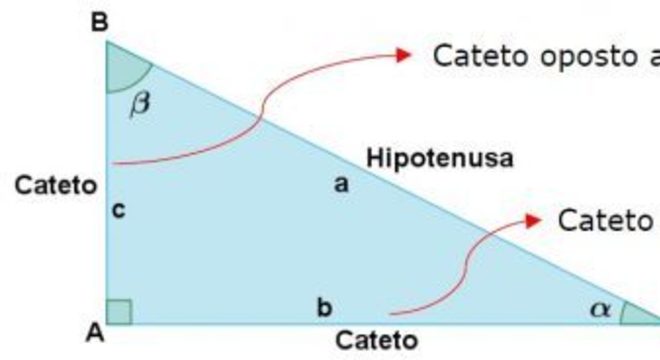
Fonte: InfoEscola
De acordo figura, pode-se concluir que:
tg (a) = (cateto oposto a α)/(cateto adjacente a α)
tg (a) = AB/AC
tg (a) = C/B
Obs.1: 1. A tangente de um ângulo agudo pode ser definida como a razão entre o seno deste ângulo e o seu cosseno. Sendo assim:
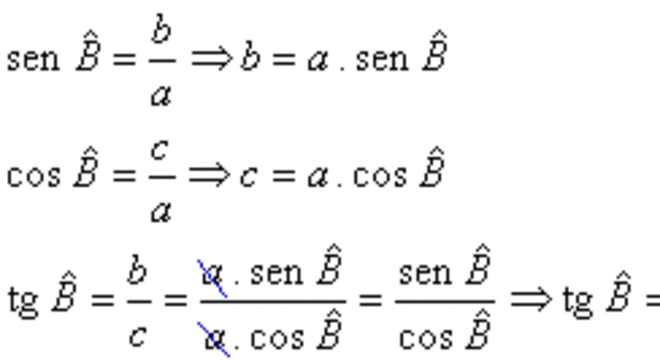
Obs.2: A tangente de um ângulo agudo é um número real positivo.
Obs.3: O seno e o cosseno de um ângulo agudo são sempre números reais positivos menores que 1, pois qualquer cateto é sempre menor que a hipotenusa.
Números Irracionais – O que são, origem e exemplos
×Tangente dos ângulos notáveis
Os valores de seno, cosseno e tangente de cada ângulo podem ser encontrados em uma tabela de razões trigonométricas ou podem ser calculados em uma calculadora científica. Portanto, é exigido que os alunos saibam esses valores para os ângulos notáveis.
São denominados ângulos notáveis aqueles calculados facilmente, assim sendo: 30°, 45° e 60°.
Confira os ângulos notáveis da tangente de acordo com a tabela abaixo:

Fonte: Guia Estudo
Função tangente
A função é definida assim:
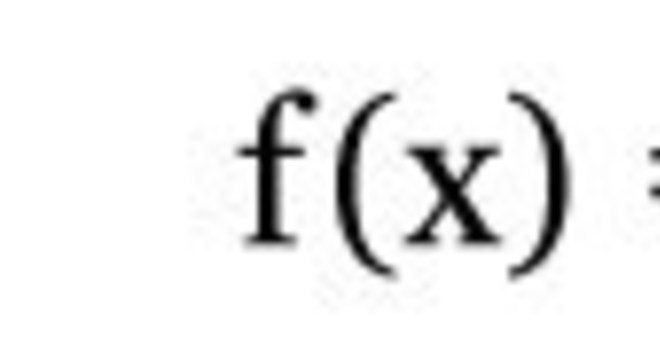
Desse modo, de acordo com o círculo trigonométrico, temos:
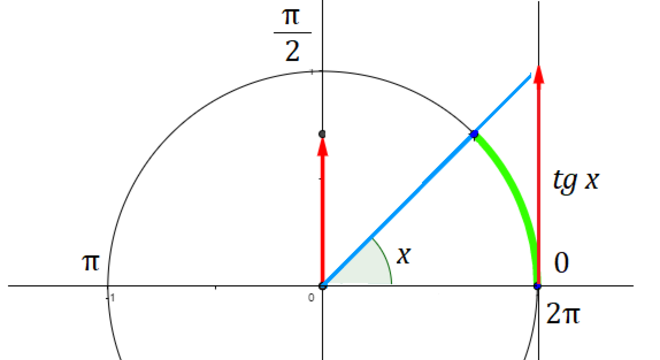
Fonte: InfoEscola
Sendo assim, para identificar uma tangente, é importante observar as seguintes características:
A função tem imagem Real, ou seja, é válida para todo x real. Ela é um ângulo sempre estará paralela ao eixo das ordenadas (y); Os quadrantes ímpares (1° e 3°) sempre terão valores positivos; Os quadrantes pares (2° e 4°) sempre terão valores negativos;Gráfico da função tangente
O gráfico da função pode ser entendido a partir da tabela abaixo:
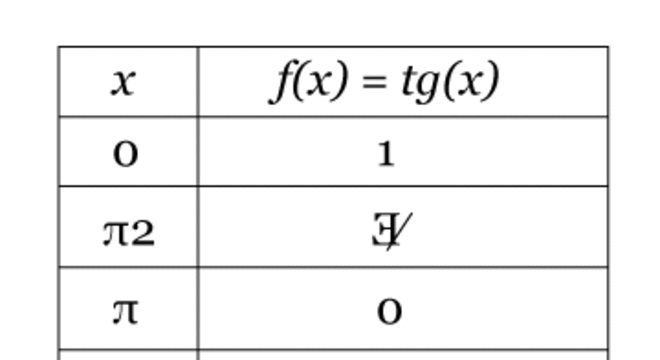
Fonte: Guia Estudo
Sendo assim, o gráfico da função fica desta maneira:
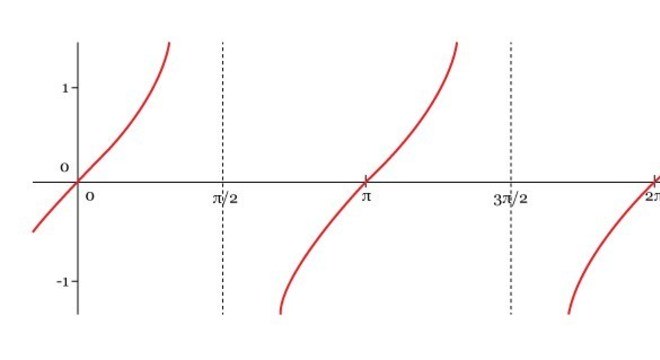
Fonte: Guia Estudo
De acordo com o gráfico, é importante nota que as retas onde a função não existe, são chamadas de assíntotas.
Ou seja, X = π/2 + kπ são assíntotas.
Lei das tangentes
Após entender a relação entre as tangentes de dois ângulos de um triângulo e os comprimentos de seus lados opostos, entenda agora a lei das tangentes:
De acordo com a lei das tangentes, considere a, b e c os comprimentos dos três lados do triângulo. E α, β e Y os ângulos opostos a estes referidos lados. Sendo assim: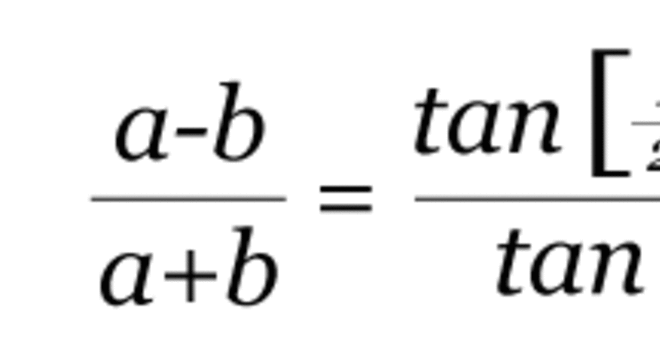
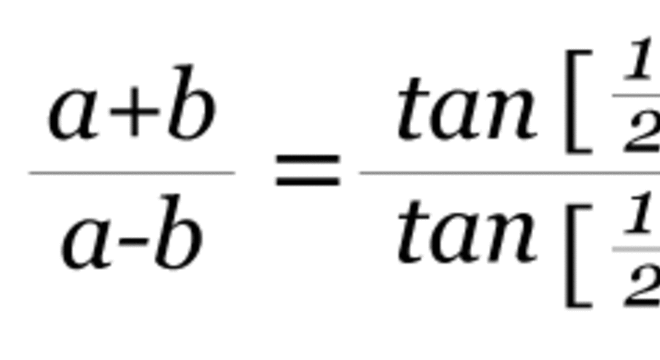
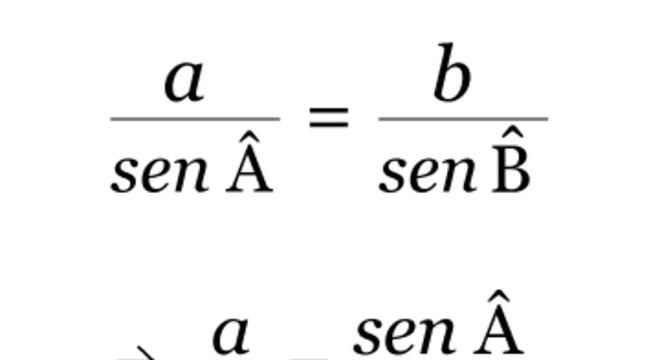
Exercício
Exemplo 1:Calcule a medida de x no seguinte triângulo, sabendo que tg(30°)= 3/ √3.
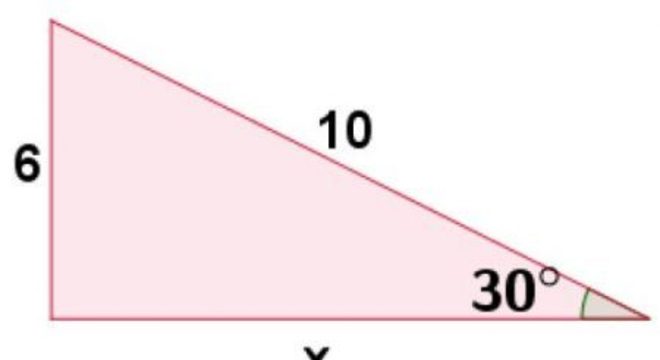
Sendo assim, chegamos ao seguinte resultado:
tg(30°) = 6/ x
3/ √3 = 6/ x
x/ √3 = 18
x = 18/ √3 . √3 / √3 = 18√3/ 3
x = 6√3
Exercício 2Em um triângulo retângulo a hipotenusa mede 10 e seus catetos medem 6 e 8. A tangente de α mede?
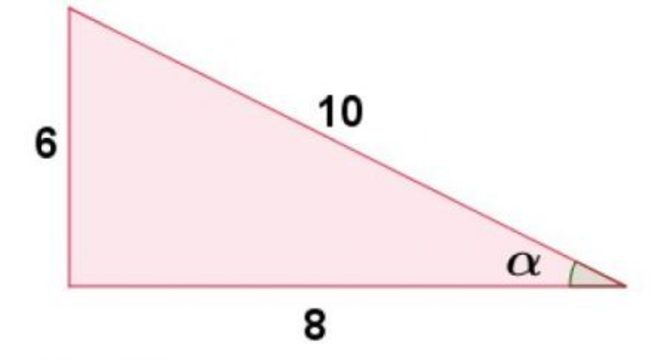
De acordo com a imagem, nós temos os três lados do triangulo, desse modo:
tg (α) = (cateto oposto a α)/(cateto adjacente a α)
tg (α) = 6/8
tg (α) = 0,75
Em conclusão, é muito importante saber dessas relações da trigonometria. Depois de ter estudado tangente, em seguida estude também sobre raízes exatas.
Fontes: InfoEscola, Educa Mais Brasil, Só Matemática
Fonte das expressões numéricas: Guia Estudo
Fonte Imagem Destaque: Pinterest
Essa matéria Tangente – Definição, gráfico da função, tabela e Lei das tangentes foi criada pelo site Conhecimento Científico.


![Primos fazem SEXO e causa polemica [VÍDEO COMPLETO E SEM TARJAS]](http://3.bp.blogspot.com/-vXjTwuHUrsE/Un_88dXnSrI/AAAAAAAADyM/wxGcIRXYVz4/w72-h72-p-k-no-nu/Sem+t%C3%ADtulo.jpg)



0 Comentários