Cone – O que é, elementos, características e medidas

Decerto, ao estudarmos Geometria nos deparamos com várias situações geométricas, alguns sólidos possuem origem e fundamentos na sua formação, um deles é o cone, figura presente no cotidiano.

O cone é uma figura geométrica espacial com formato de pirâmide que faz parte dos estudo da geometria espacial. Certamente, é esta é uma figura tridimensional, disposto no plano através das coordenadas x, y e z.

Dado um círculo de centro O e raio R no plano B, e um ponto P fora do plano. Esta figura será formada por segmentos de reta unindo o ponto P aos pontos do círculo.

Elementos do cone

Decerto, essa figura é formada pelos seguintes elementos:

Raio da base: é o raio do círculo que forma a base; Geratriz: são os segmentos de retas em um ponto da circunferência até o vértice superior; Vértice: possui um vértice que fica oposto a base circular. Eixo de rotação: é a reta que parte do centro da base até o vértice superior; é também o tamanho da reta que define a altura do cone.

Área da circunferência – O que é, como calcular e exemplos na prática

×

Classificação dos cones

Cone -Respectivamente cone reto, oblíquo e equilátero Como é essa figura? Conhecimento Científico

Respectivamente cone reto, oblíquo e equilátero – Fonte: Matemática básica

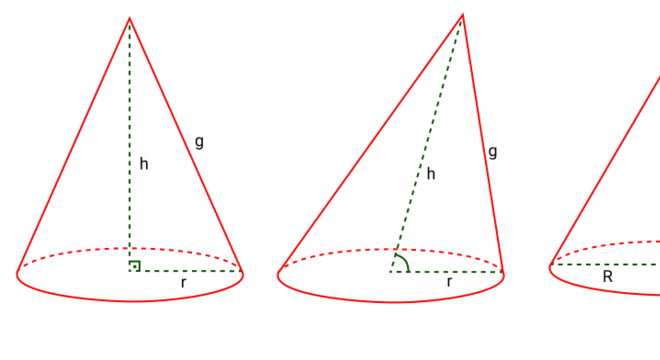
Certamente, essa figura pode ser classificado em três categorias: reto, oblíquo e equilátero.

Cone reto

Por certo, o cone reto é formado por uma base circular e uma reta ligada ao vértice superior. A reta é perpendicular a base e liga o centro da circunferência. Além disso, o eixo é perpendicular à base, ou seja, a altura e o centro da base do cone formam um ângulo de 90º, donde todas as geratrizes são congruentes entre si e.

Geratrizes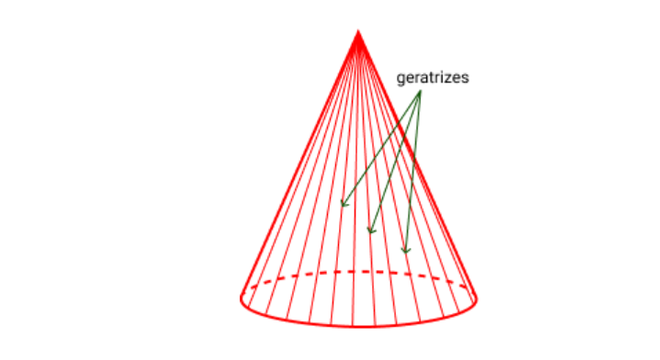

Cone - Como é essa figura? Conhecimento Científico

Fonte: Matemática básica

Esta figura tem toda a sua lateral formada por retas chamadas de geratrizes (g). As geratrizes, basicamente são retas que ligam os pontos da circunferência até o vértice superior. Assim, os pontos das geratrizes na linha da circunferência formam um conjunto chamado de diretriz. Decerto, recebe esse nome pois fornecem a direção para as geratrizes.

O eixo do cone, perpendicular a base, a geratriz e a base formam um triângulo retângulo. Assim, podemos aplicar o Teorema de Pitágoras obtendo a seguinte relação: g² = h² + r².

Cone é um sólido de revolução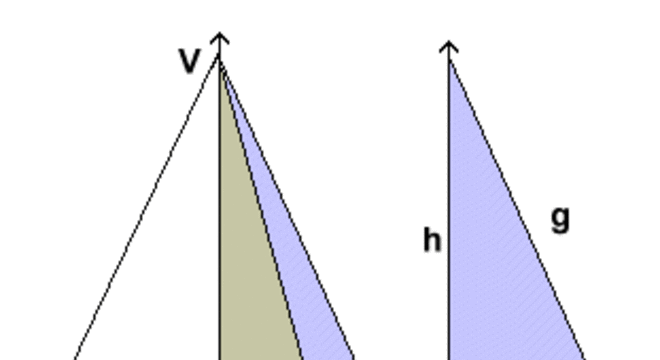

Cone - Como é essa figura? Conhecimento Científico

Cone de revolução – Fonte: A casinha da matemática

Nos cones retos, a reta perpendicular a base, a base e a geratriz formam um triângulo retângulo. Assim, podemos dizer que o cone é formado por um triângulo que gira em torno de um dos catetos. Essa figura é considerado um sólido de revolução, pois pode ser obtido através de uma rotação no plano de curva, girando em torno de uma reta no mesmo plano.

Cone Oblíquo

Esse tipo de figura, tem uma reta que parte da base e liga o vértice superior não é perpendicular a base. Assim, a reta e a base não forma um ângulo reto.

Cone equilátero

Decerto, um cone circular reto é equilátero quando a seção meridiana é um triângulo equilátero. Dessa forma, a geratriz é igual a duas vezes o raio da base circular, ou seja, a medida da geratriz é igual ao diâmetro da base. E a altura do cone é dada pela fórmula: h = R√3.

Área

Certamente, antes de calcularmos a área, primeiramente é necessário calcular a área lateral e a área da base.

Área lateral

Então, área lateral é formada pela geratriz e é dada ela seguinte fórmula:

Al = π . r . g

π: é o número pi que é igual a 3,14;

r: é a medida do raio da circunferência da base;

g: é a medida da geratriz.

Área da base

Assim, a área da base é equivalente a área da circunferência. Então podemos usar a seguinte fórmula:

Ab = π . r²

π: é o número pi;

r: é o raio da circunferência.

Área total

Decerto, a área total é a soma da área da base e da área da lateral. Assim, podemos usar a seguinte fórmula:

At = π . r . (g + r)

π: é o número pi;

r: é a medida do raio da circunferência da base;

g: é a medida da geratriz.

Volume

Cone - Como é essa figura? Conhecimento Científico

Fonte: área do cone

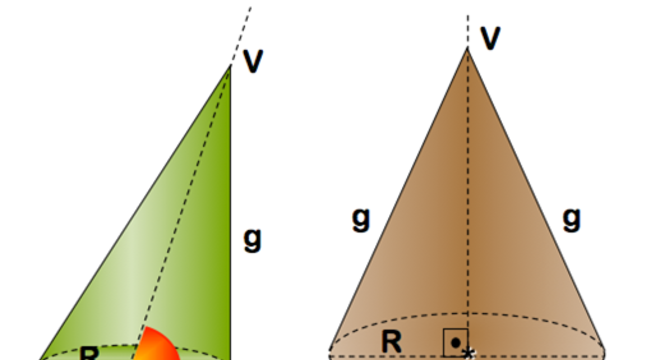
Certamente, o volume dessa figura é dado pelo produto da área da base pela altura divido por três. Assim, podemos calcular o volume do cone pela seguinte fórmula:

V = 1⁄3 . π . r² . h

π: é número pi, 3,14;

r: é a medida do raio;

h: é a medida da altura.

Fonte: Matemática básica, Brasil escola, Toda matéria.

Imagem destacada: Matemática básica

Essa matéria Cone – O que é, elementos, características e medidas foi criada pelo site Conhecimento Científico.