Primeiramente, as operações com conjuntos são as operações feitas com os elementos que formam uma coleção. Em resumo, são elas: união de conjuntos, intersecção de conjuntos, diferença entre conjuntos e conjunto complementar.
Sendo assim, de acordo com a matemática, os conjuntos representam a reunião de diversos objetos, realizado com determinada quantidade e que segue uma mesma lógica.
Além disso, quando os elementos que formam o conjunto são números, são chamados de conjuntos numéricos.
Sendo eles:
Números Naturais (N) Números Inteiros (Z) Números Racionais (Q) Números Irracionais (I) Números Reais (R)Contudo, existem também conjuntos não numéricos, como exemplo o conjunto de letras do alfabeto: L = {a, b, c, d, e, f, g, h … x, y e z}
Mas afinal, o que é um conjunto e como ele é representado?
Representação dos conjuntos
Inicialmente, como visto no último exemplo, a representação das operações com conjuntos pode ser por nomeação dos elementos. Exemplo: Conjunto de cores primárias: C = {vermelho, amarelo e azul}
Além disso, outras duas são utilizadas com frequência:
Por compreensão – nesse modo de representação é expressa uma propriedade característica comum aos elementos. Desse modo: C = {cores primárias}
Por diagrama – o diagrama de Venn, é traçado a partir de coleções de curvas fechadas dentro de um plano e no interior das curvas encontram-se os elementos. Assim sendo: Conjunto dos números primários: A = {1, 2, 3, 4, 5, 6}
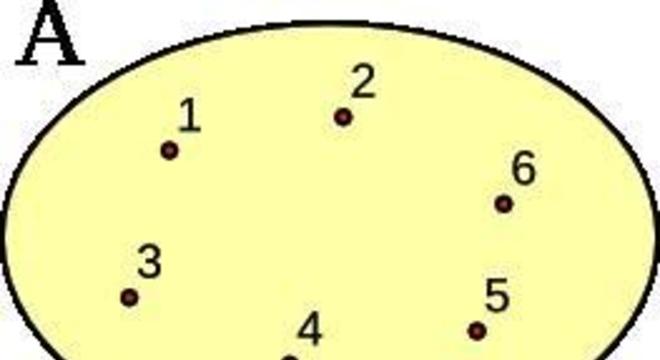
Fonte: Doc Player
Cosseno – Definição, gráfico da função, tabela e Lei dos Cossenos
×Operações com conjuntos
Acima de tudo, a Teoria dos Conjuntos estabelece alguns símbolos e é necessário entende-los para indicar relação entre os elementos.
Sendo assim, confira nas tabelas os principais símbolos:
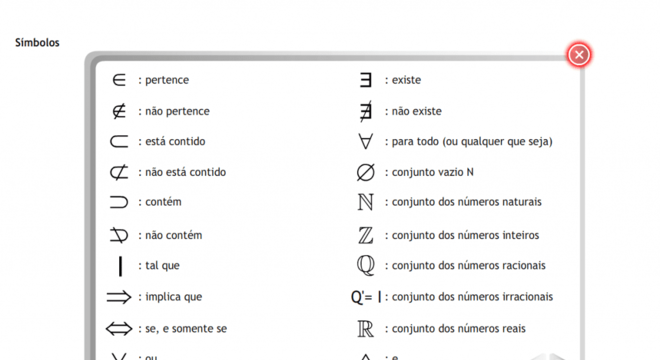
Fonte: Passei Direto
Por fim, como resultado disso, temos:

Fonte: Prof Janice Blog
Desse modo, depois de ter entendido o que é conjunto, como é representado e seus símbolos, vamos para o que interessa. Em seguida, veremos os tipos de operações com conjuntos.
União de conjuntos
A união de conjuntos corresponde a junção dos elementos dos conjuntos dados, ou seja, é o conjunto formado pelos elementos de um conjunto, mais os elementos dos outros conjuntos.
No caso dos elementos que se repetem, eles aparecerão uma única vez no conjunto união.
Em resumo, basta unir os elementos de A com os de B.
Por fim, para representar a união usamos o símbolo U.
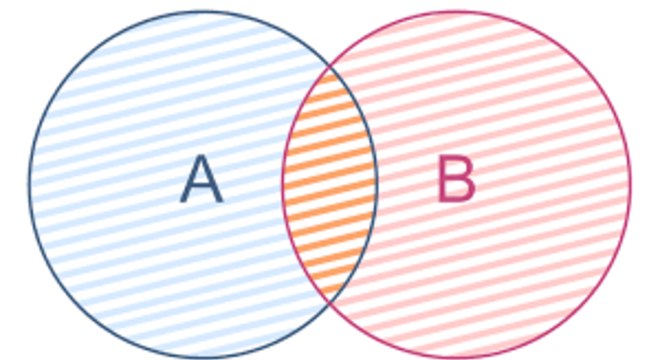
Fonte: Matika
Exemplo:
Dados os conjuntos A = {0, 1, 2, 3, 4, 5, 6, 7} e B = {0, 2, 4, 6, 8}, represente o conjunto união (A U B).
De acordo com o que vimos anteriormente, para encontrar o conjunto união, basta juntar os elementos dos dois conjuntos dados.
Portanto, o conjunto união será:
(A U B) = {0, 1, 2, 3, 4, 5, 6, 7, 8}
Intersecção de conjuntos
Acima de tudo, na Teoria dos conjuntos, a interseção ou intersecção, é um conjunto de elementos que, simultaneamente, pertencem a dois ou mais conjuntos.
Dessa maneira, a intersecção dos conjuntos é representado pelo símbolo ∩.
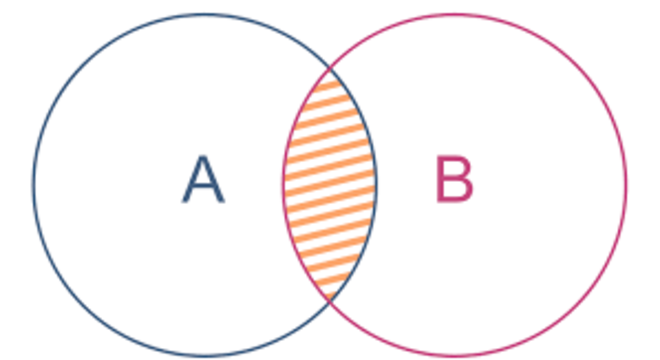
Fonte: Matika
Exemplo:
Dados os conjuntos A = {0, 2, 3, 4, 5, 6, 7} e B = {0, 2, 4, 6, 8}, represente o conjunto intersecção (A ∩ B).
Devemos identificar os elementos comuns nos conjuntos dados que, neste caso, são os elementos A e B.
Desse modo, o conjunto intersecção ficará: (A ∩ B) = {0, 2, 4, 6, 8}
Obs.1: O conjunto que não possui nenhum elemento é chamado de conjunto vazio. Sendo assim, ele pode ser represento de duas formas: A = { } ou A = Ø
Obs.2: E quando dois conjuntos não apresentam elementos em comum, dizemos que a intersecção entre eles é um conjunto vazio.
Sendo assim, esses conjuntos são chamados de disjuntos: A ∩ B = Ø
Diferença entre conjuntos
A diferença entre conjuntos corresponde aos elementos de um conjunto que não estão no outro conjunto.
Sendo assim, a diferença entre A e B, é dada pelos elementos que pertencem a A e não pertencem a B.
Portanto, o conjunto diferença é indicado por A – B (lê-se A menos B).
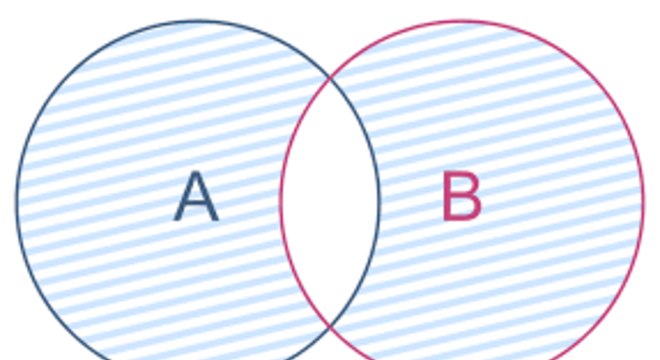
Fonte: Matika
Exemplo:
Em vista disso, considere os conjuntos A = {0, 1, 2, 3, 4, 5, 6, 7} e B = {0, 1, 2, 3, 4, 6, 7}, represente a diferença entre conjuntos (A – B).
Em conclusão, devemos identificar os elementos que pertencem ao conjunto A, e que não pertencem no conjunto B.
Desse modo, a diferença entre conjuntos será: (A – B) = {5}
Conjuntos complementares
Essa operação relaciona-se com a diferença entre conjuntos. Sendo assim, considerando os conjuntos A e B, o complemento relativo de A em relação a B, ou seja, a diferença de B e A, é o conjunto de elementos de B que não estão em A.
Portanto, a diferença entre os conjuntos, B – A, é chamada de complementar de A em relação a B.
Contudo, quando temos um conjunto B, tal que B está contido em A, a diferença A – B, é o conjunto de elementos de A que não estão em B.
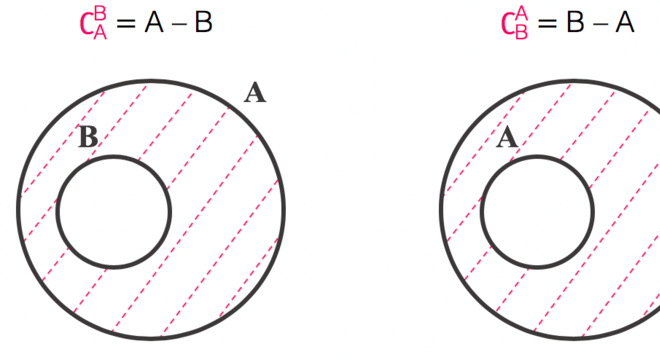
Fonte: Blog Professor Ferreto
Exemplo:
Considere os conjuntos A = {0, 1, 2, 3, 4, 5} e B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.
Sendo assim, o complementar de A em relação a B
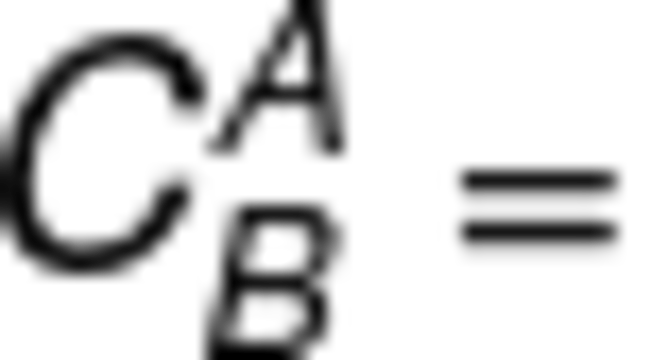
é: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10} – {0, 1, 2, 3, 4, 5} = {6, 7, 8, 9, 10}
Propriedades da União e da Intersecção
Dados três conjuntos A, B e C, as seguintes propriedades são válidas:
Propriedade comutativa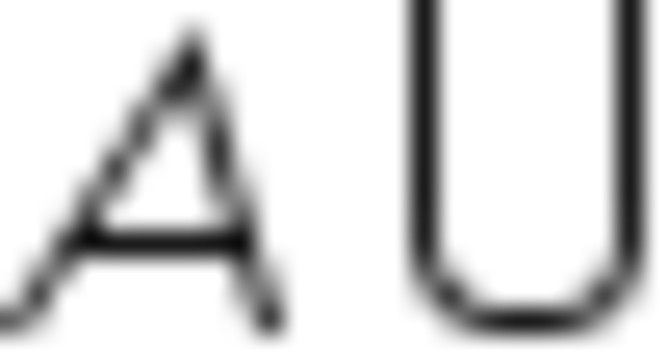
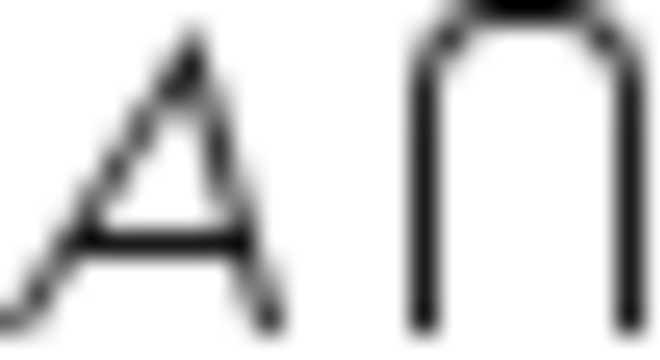
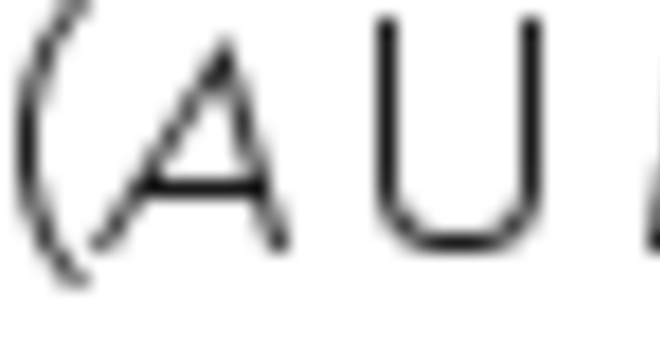
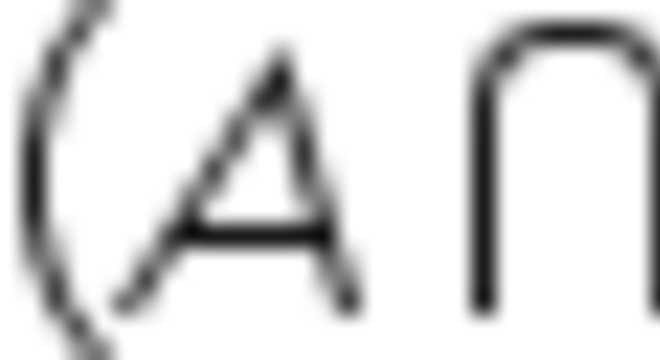
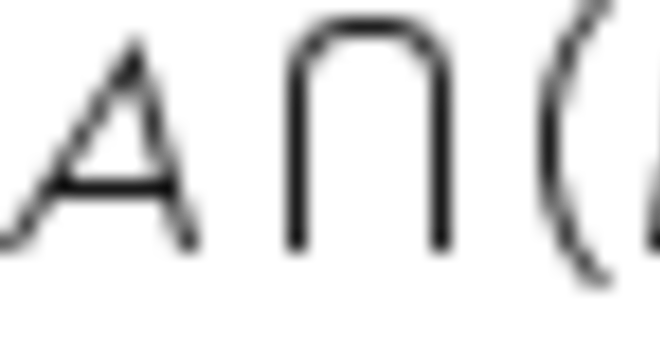
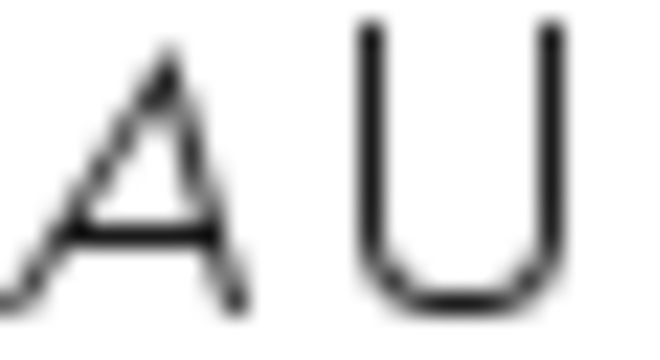
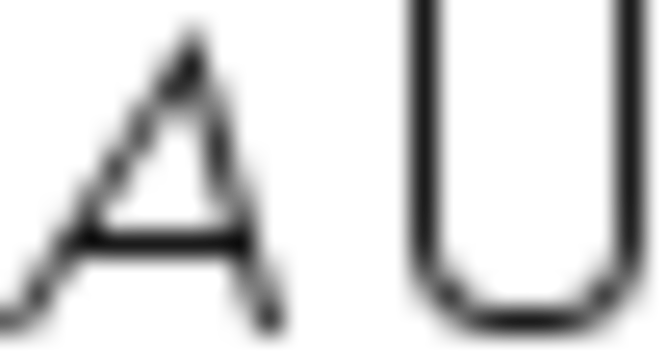
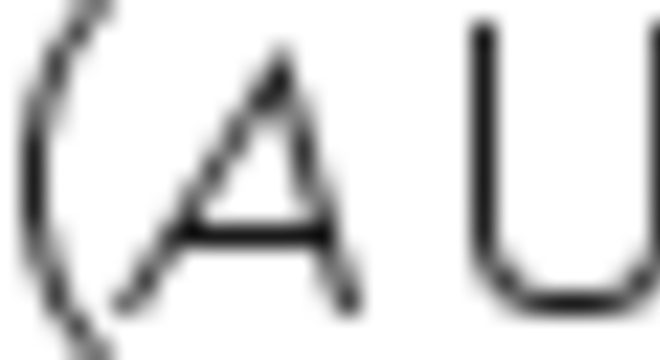
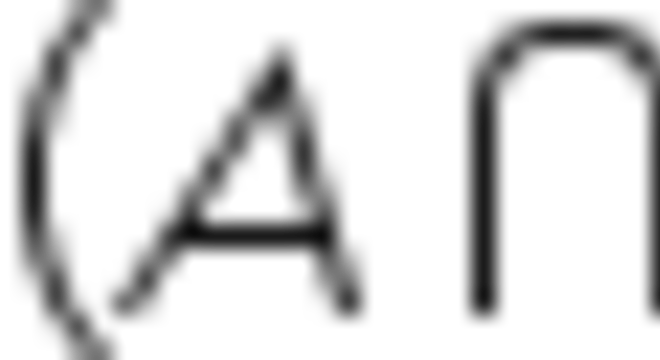
Leis de Morgan
Nesse meio tempo, considerando os conjuntos pertencentes a um universo U, tem-se:
1°. O complementar da união é igual à intersecção dos complementares:
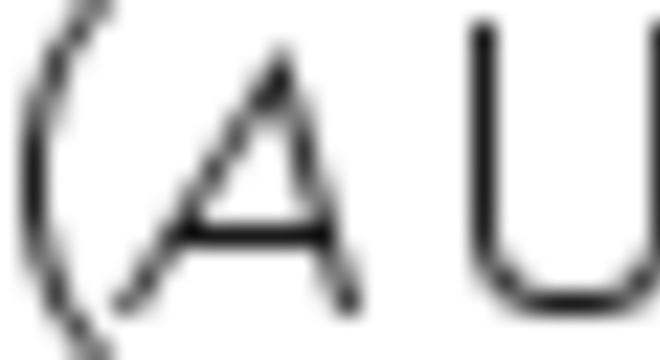
2°. O complementar da intersecção é igual à união dos complementares:
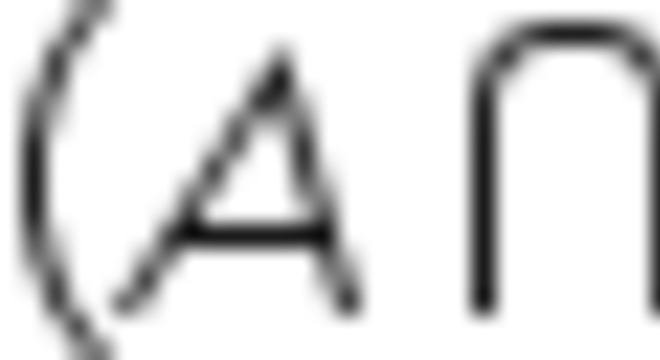
Exercícios
Exercício 1:Considere os conjuntos A = {a, b, c, d, e, f} e B ={d, e, f, g, h, i}. Determine (A – B) U (B – A).
Solução:
Inicialmente determinaremos os conjuntos A – B e B – A e, em seguida, realizaremos a união entre eles.
A – B = {a, b, c, d, e, f} – {d, e, f, g, h, i}
A – B = {a, b, c}
B – A = {d, e, f, g, h, i} – {a, b, c, d, e, f}
B – A = {g, h, i}
Sendo assim, (A – B) U (B – A) é:
{a, b, c} U {g, h, i}
{a, b, c, g, h, i}
Exercício 2:Suponhamos que A U B = {a, b, c, d, e, f, g, h}, A ∩ B = {d, e} e A – B = {a, b, c}, então:
a) B = {f, g, h}
b) B = {d, e, f, g, h}
c) B = { }
d) B = {d, e}
e) B = {a, b, c, d, e}
Solução:
Alternativa B.
Nesse sentido, dispondo os elementos no diagrama de Venn-Euler, segundo o enunciado, temos:
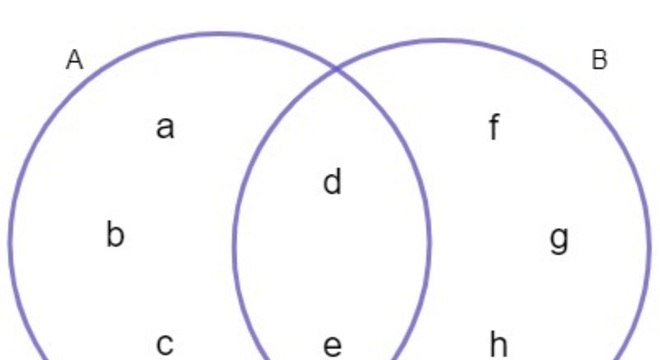
Portanto, o conjunto B = {d, e, f, g, h}.
Gostou de saber das operações com conjuntos? Em seguida veja sobre os conjuntos numéricos que existem.
Fontes: Brasil Escola, Toda Matéria, Educa Mais Brasil
Fonte das expressões numéricas: Toda Matéria
Fonte Imagem Destaque: Estudo Kids
Essa matéria Operações com conjuntos – Representação e os tipos foi criada pelo site Conhecimento Científico.


![Primos fazem SEXO e causa polemica [VÍDEO COMPLETO E SEM TARJAS]](http://3.bp.blogspot.com/-vXjTwuHUrsE/Un_88dXnSrI/AAAAAAAADyM/wxGcIRXYVz4/w72-h72-p-k-no-nu/Sem+t%C3%ADtulo.jpg)



0 Comentários